设集合 ,集合
,集合 ,则
,则
A. |
B. |
C. |
D. |
设f(x)=tan3x+ tan3x
tan3x ,则f(x)为
,则f(x)为
A.周期函数,最小正周期为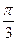 |
B.周期函数,最小正周期为 |
C.周期函数,最小正周期为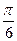 |
D.非周期函数 |
如果复数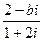 (其中
(其中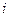 为虚数单位,b为实数)的实部和虚部都互为相反数,那么b等于
为虚数单位,b为实数)的实部和虚部都互为相反数,那么b等于
A. |
B.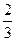 |
C. |
D.2 |
定义集合运算:A⊙B={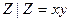 ,x∈A,y∈B},设集合A={
,x∈A,y∈B},设集合A={ ,0,1},B=
,0,1},B=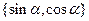 ,则集合A⊙B的所有元素之和为
,则集合A⊙B的所有元素之和为
| A.1 | B.0 | C. |
D. |
(本小题满分16分)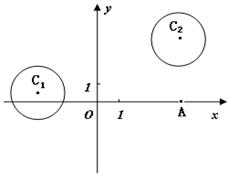
在平面直角坐标系 中,已知圆
中,已知圆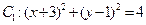 和圆
和圆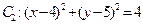 .
.
(1)若直线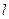 过点
过点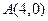 ,且被圆
,且被圆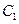 截得的弦长为
截得的弦长为 ,求直线
,求直线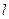 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线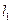 和
和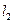 ,它们分别与圆
,它们分别与圆 和圆
和圆 相交,且直线
相交,且直线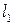 被圆
被圆 截得的弦长与直线
截得的弦长与直线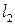 被圆
被圆 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
(上海文,18)过圆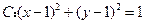 的圆心,作直线分
的圆心,作直线分
别交x、y正半轴于点A、B,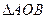 被圆分成四部分(如图),
被圆分成四部分(如图),
若这四部分图形面积满足 则直线AB有()
则直线AB有()
| A.0条 | B.1条 | C. 2条 | D.3条 |