设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1= , λ2=
, λ2= ,λ3=
,λ3=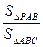 ,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=(
,定义f(P)=(λ1, λ, λ3),若G是△ABC的重心,f(Q)=(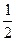 ,
,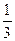 ,
, ),则
),则
| A.点Q在△GAB内 | B.点Q在△GBC内 |
| C.点Q在△GCA内 | D.点Q与点G重合 |
对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有().
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)≤2f(1) |
| C.f(0)+f(2)≥2f(1) | D.f(0)+f(2)>2f(1) |
已知正项数列 的前
的前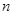 项和为
项和为 ,且
,且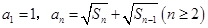 ,则数列
,则数列 的通项公式为
的通项公式为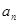 =()
=()
A. |
B.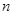 |
C.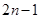 |
D.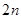 |
已知定义在 上的函数
上的函数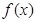 满足:
满足: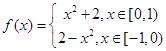 ,且
,且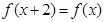 ,
,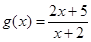 ,则方程
,则方程 在区间
在区间 上的所有实根之和为()
上的所有实根之和为()
| A.-7 | B.-8 | C.-6 | D.-5 |
将函数 的图象向左平移
的图象向左平移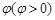 个单位后,所得到的图象对应的函数为奇函数,则
个单位后,所得到的图象对应的函数为奇函数,则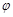 的最小值为()
的最小值为()
A.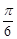 |
B. |
C. |
D.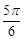 |
已知双曲线 (
(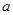 >0,
>0,  >0)的离心率为2,一个焦点与抛物线
>0)的离心率为2,一个焦点与抛物线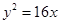 的焦点相同,则双曲线的渐近线方程为()
的焦点相同,则双曲线的渐近线方程为()
A. |
B. |
C. |
D.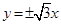 |