如图所示,某货场而将质量为的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径。地面上紧靠轨道次排放两声完全相同的木板,长度均为=2,质量均为,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为,木板与地面间的动摩擦因数。(最大静摩擦力与滑动摩擦力大小相等,取=10)
(1)求货物到达圆轨道末端时对轨道的压力。
(2)若货物滑上木板4时,木板不动,而滑上木板时,木板开始滑动,求应满足的条件。
(3)若,求货物滑到木板末端时的速度和在木板上运动的时间。

如图所示,匀强磁场方向垂直纸面向里,磁感应强度B=0.20T,OCA金属导轨
与OA金属直导轨分别在O点和A点接一阻值为R1=3.0Ω和R2=6.0Ω体积可忽
略的定值电阻,导轨OCA的曲线方程为 y=1.0sin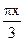 (m),金属棒ab平行于y 轴,
(m),金属棒ab平行于y 轴,
长为1.5m,以速度v="5.0" m/s水平向右匀速运动(b点始终在Ox轴上),设金属
棒与导轨接触良好,摩擦不计,电路中除了电阻R1和R2外,其余电阻均不计,求: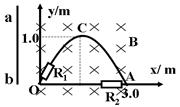
(1)金属棒在导轨上运动时R1的最大功率
(2)金属棒在导轨上从x=0到x=3m的运动过程中,外力必须做的功。
如图所示,线圈匝数n=100匝,面积S=50cm2,线圈总电阻r=10Ω,外电路总电阻R=40Ω,沿轴向匀强磁场的磁感应强度由B=0.4T在0.1s内均匀减小为零再反向增为B=0.1T,求(1)磁通量的变化率为多少?(2)感应电流大小为多少?(3)线圈的输出功率为多少?
已知湖宽40m,湖的A、B两岸各高出水面分别为2m和1m,某人想通过在B岸观
察A岸边的一株树的倒影,测出这树的高度。如果人眼离地高度为1.6m,当人
的观察位置到岸边B的距离超过6.4m时,就看不到树梢的倒影,试作出上述情
况的光路图,并计算树高。
如图所示一列横波的某时刻波形图,质点A处于波峰位置,如质点A再经过0.1秒将第一次到达平衡位置。试求这列波的波长λ,频率f和波速v各是多少?
如图学校有一台应急备用发电机,内阻为r=1 Ω,升压变压器匝数比为1∶4,降压变压器的匝数比为4∶1,输电线的总电阻为R=4 Ω,全校22个教室,每个教室用“220 V、40 W”的灯6盏,要求所有灯都正常发光,则:
(1)发电机的输出功率多大?
(2)发电机的电动势多大?
(3)输电线上损耗的电功率多大?