如图甲所示，建立坐标系，两平行极板、垂直于轴且关于轴对称，极板长度和板间距均为l，第一四象限有磁场，方向垂直于平面向里。位于极板左侧的粒子源沿轴间右连接发射质量为、电量为、速度相同、重力不计的带电粒子在时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）。
已知=0时刻进入两板间的带电粒子恰好在时，刻经极板边缘射入磁场。上述、、、、为已知量。（不考虑粒子间相互影响及返回板间的情况）
（1）求电压的大小。
（2）求时进入两板间的带电粒子在磁场中做圆周运动的半径。
（3）何时把两板间的带电粒子在磁场中的运动时间最短？求此最短时间。
在运动的升降机中天花板上用细线悬挂一个物体Ａ，下面吊着一个轻质弹簧秤（弹簧秤的质量不计），弹簧秤下吊着物体Ｂ，如图所示。物体Ａ和Ｂ的质量相等，都为m＝5kg，某一时刻弹簧秤的读数为40 N，设ｇ＝10m/s2。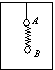
求细线的拉力。
若将细线剪断，求在剪断细线瞬间物体Ａ和B的加速度的大小和方向。
均匀木板AB长L＝1.6m，质量M＝2kg，如图所示，转轴0距地面高度h＝0.6m，木板AO部分长L＝1m．有一滑块质量m＝1kg，以初速度V0＝8m/s沿木板上滑．滑块与木板间动摩擦因数μ＝0.5，g取10m/
求：
(1)滑块滑到什么位置时，木板开始翻动?
(2)翻转时滑块的速度多大?
(3)滑块从起始时刻到木板翻转时刻用的时间?
已知地球半径R＝6.4×
km，试求在赤道上空相对于地球静止的同步卫星距地面的高度h，并求同步卫星发射回地球的信号可覆盖的范围(以对地心的圆心角表示)．
已知地球质量为M、半径为R，万有引力常量G．卫星在地球表面绕地球做匀速圆周运动所需的速度称为第一宇宙速度v1,卫星从地面发射，恰好能脱离地球引力束缚的速度称为第二宇宙速度v2，已知v2=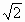
v1．根据以上条件，并以卫星脱离地球引力时的引力势能为0，求质量为m的卫星在地球表面时的引力势能．(忽略空气阻力的影响)
如图所示，风洞实验室中可产生水平方向的，大小可调节的风力．现将一套有小球的细直杆放入风洞实验室．小球孔径略大于细杆直径．
(1)当杆在水平方向上固定时，调节风力的大小，使小球在杆上作匀速运动，这时小球所受的风力为小球所受重力的0.5倍，求小球与杆间的动摩擦因数．
(2)保持小球所受风力不变，使杆与水平方向间夹角为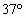
固定，则小球从静止出发在细杆上滑下距离s所需时间为多少？(sin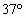＝0.6，cos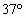＝0.8)