(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)= 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
在极坐标系中,圆C的方程为ρ=2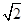 sin
sin ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的方程为y=2x+1,判断直线l和圆C的位置关系.
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的方程为y=2x+1,判断直线l和圆C的位置关系.
在极坐标系中,设圆ρ=3上的点到直线ρ(cosθ+ sinθ)=2的距离为d.求d的最大值.
sinθ)=2的距离为d.求d的最大值.
求以点A(2,0)为圆心,且过点B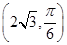 的圆的极坐标方程.
的圆的极坐标方程.
如图,AB是半径为1的圆的一条直径,C是此圆上任意一点,作射线AC,在AC上存在点P,使得AP·AC=1,以A为极点,射线AB为极轴建立极坐标系.
(1)求以AB为直径的圆的极坐标方程;
(2)求动点P的轨迹的极坐标方程;
(3)求点P的轨迹在圆内部分的长度.
求极坐标方程分别为ρ=cosθ与ρ=sinθ的两个圆的圆心距.