（本小题满分14分） 如图：在四棱锥P-ABCD中，底面为正方形，PC与底面ABCD垂直（图1），图2为该四棱锥的主视图和侧视图，它们是腰长为6cm的全等的等腰直角三角形.
|
|
，
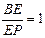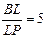，M、N分别为棱PA 、PD的中点，问在底面正方形的对角线AC上是否存在一点F，使EF//平面LMN. 若存在，请具体求出CF的长度；若不存在，请说明理由.
已知函数
在
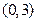内有极值，求实数
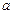的范围。
.设函数
且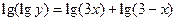
。
（Ⅰ）求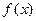
的解析式及定义域。（Ⅱ）求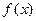的值域。
已知函数
.
（Ⅰ）当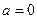
时，求曲线
在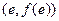
处的切线方程（
）
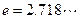（Ⅱ）已知
为函数
的极值点，求函数的单调区间。
（本小题满分10分）选修4-5：不等式选讲
已知函数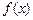
=|x-2|
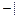x-5|．
（I）证明：
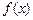≤≤3；
（II）求不等式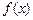≥x2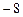
x+15的解集．
（本小题满分10分）选修4-4：坐标系统与参数方程
在平面直角坐标系xOy中，曲线C1的参数方程为
（
为参数），曲线C2的参数方程为
（
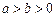，为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，射线l：θ=
与C1，C2各有一个交点．当=0时，这两个交点间的距离为2，当=
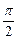时，这两个交点重合．
（I）分别说明C1，C2是什么曲线，并求出a与b的值；
（II）设当=
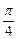时，l与C1，C2的交点分别为A1，B1，当=
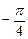时，l与C1，C2的交点为A2，B2，求四边形A1A2B2B1的面积．