某种食品是经过
、
、
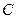三道工序加工而成的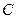，、、工序的产品合格率分别为
、
、
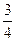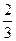．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；有两道合格为二等品；其它的为废品，不进入市场．
（Ⅰ）正式生产前先试生产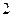
袋食品，求这２袋食品都为废品的概率；
（Ⅱ）设
为加工工序中产品合格的次数，求的分布列和数学期望．
已知
为定义在R上的偶函数，
为实常数，
（1）求的值；
（2）若已知
为定义在R上的奇函数，判断并证明函数
的奇偶性。
已知集合
，
，求实数
的值。
(14分)已知数列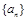
的首项
，
，
…．
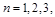(1)数列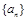的通项公式；
(2)求数列
的前
项和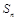
．
(14分)等差数列{an}中，公差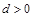
，其前
项和为
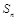，且满足
，
。
(1)求数列{an}的通项公式；
(2)构造一个新的数列{bn}，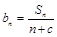
，若{bn}也是等差数列，求非零常数
．
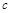(14分)一农民有基本农田2亩，根据往年经验，若种水稻，则每季每亩产量为400公斤，但需成本240元；若种花生，则每季每亩产量为100公斤，但成本只需80元。种花生每公斤可卖5元，稻米每公斤卖3元．现该农民手头有400元，两种作物各种多少，才能获得最大收益？