设椭圆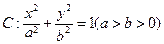 的一个顶点与抛物线
的一个顶点与抛物线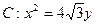 的焦点重合,
的焦点重合,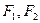 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率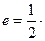 且过椭圆右焦点
且过椭圆右焦点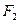 的直线
的直线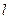 与椭圆C交于
与椭圆C交于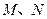 两点.
两点.
(1)求椭圆C的方程;
(2)是否存在直线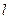 ,使得
,使得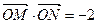 .若存在,求出直线
.若存在,求出直线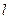 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(3)若AB是椭圆C经过原点O的弦, MN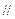 AB,求证:
AB,求证: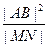 为定值.
为定值.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
序号 |
分组睡眠时间 |
组中值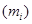 |
频数 (人数) |
频率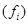 |
| 1 |
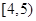 |
4.5 |
80 |
( ) |
| 2 |
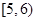 |
5.5 |
520 |
0.26 |
| 3 |
 |
6.5 |
600 |
0.30 |
| 4 |
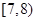 |
7.5 |
( ) |
( ) |
| 5 |
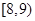 |
8.5 |
200 |
0.10 |
| 6 |
 |
9.5 |
40 |
0.02 |
(1)求出表中空白处的数据,并将表格补充完整;
(2)画出频率分布直方图;
(3)为了对数据举行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图,求输出的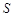 值。
值。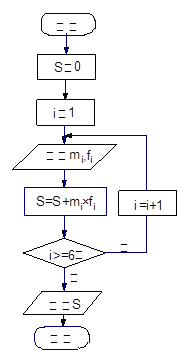
如图,已知在侧棱垂直于底面三棱柱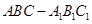 中,
中,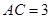 ,
,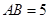 ,
,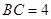 ,
,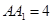 ,点
,点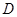 是
是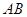 的中点.
的中点.
(1)求证: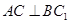 ;
;
(2)求证:
(3)求三棱锥 的体积.
的体积.
|
已知圆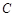 :
: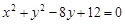 ,直线
,直线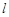 经过点
经过点 ,
,
(1)求以线段 为直径的圆
为直径的圆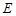 的方程;
的方程;
(2)若直线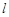 与圆
与圆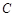 相交于
相交于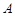 ,
,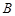 两点,且
两点,且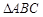 为等腰直角三角形,求直线
为等腰直角三角形,求直线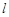 的方程.
的方程.
设函数 的最小正周期为
的最小正周期为
(1)求 的值;
的值;
(2)若函数 的图像是由
的图像是由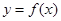 的图像向右平移
的图像向右平移 个单位长度得到,求
个单位长度得到,求 的单调增区间.
的单调增区间.
已知函数 ,
,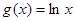 .
.
(1)求函数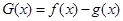 的极值;(2)若
的极值;(2)若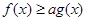 恒成立,求实数
恒成立,求实数 的值;
的值;
(3)设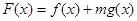
 有两个极值点
有两个极值点 、
、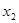 (
(

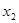 ),求实数
),求实数 的取值范围,并证明
的取值范围,并证明 .
.