命题①空间直线a,b,c,若a∥b,b∥c则a∥c
②非零向量 ,若
,若 ∥
∥ ,
, ∥
∥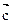 则
则 ∥
∥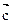
③平面α、β、γ若α⊥β,β⊥γ,则α∥γ
④空间直线a、b、c若有a⊥b,b⊥c,则a∥c
⑤直线a、b与平面β,若a⊥β,c⊥β,则a∥c
其中所有真命题的序号是( )
| A.①②③ | B.①③⑤ | C.①②⑤ | D.②③⑤ |
已知命题p:$m∈R,sinm=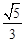 ,命题
,命题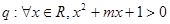 恒成立.若
恒成立.若 为假命题,则实数
为假命题,则实数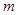 的取值范围为()
的取值范围为()
A.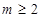 |
B.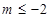 |
C.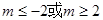 |
D.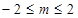 |
给出下列结论:在回归分析中可用
(1)可用相关指数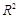 的值判断模型的拟合效果,
的值判断模型的拟合效果,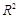 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数 的值判断模型的拟合效果,
的值判断模型的拟合效果, 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的是()
| A.(1)(3)(4) | B.(1)(4) |
| C.(2)(3)(4) | D.(1)(2)(3) |
.若h~B(2, p),且 ,则
,则 ()
()
A. |
B. |
C. |
D. |
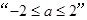 是“实系数一元二次方程
是“实系数一元二次方程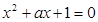 有虚根”的()
有虚根”的()
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
.9名乒乓球运动员,男5名,女4名,现要从中选出2名男队员、2名女队员进行混合双打比赛,不同的配对方法共有()
| A.60种 | B.84种 | C.120种 | D.240种 |