已知数列 满足
满足 ,
,
 。
。
(1)求数列 的通项公式;
的通项公式;
(2)求使得 的正整数
的正整数 的集合M。
的集合M。
(本小题满分10分)
有两颗正四面体的玩具,其四个面上分别标有数字1,2,3,4,下面做投掷这两颗正四面体玩具的试验:用 表示结果,其中
表示结果,其中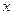 表示投掷第1颗正四面体玩具落在底面的数字,
表示投掷第1颗正四面体玩具落在底面的数字,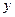 表示投掷第2颗正四面体玩具落在底面的数字。
表示投掷第2颗正四面体玩具落在底面的数字。
(1)写出试验的基本事件;
(2)求事件“落在底面的数字之和大于3”的概率;
(3)求事件“落在底面的数字相等”的概率。
(本小题满分12分)
在股票市场上,投资者常参考股价(每一股的价格)的某 条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式
条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式
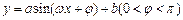 来描述,从C点走到今天的D点,是震荡筑底阶段,而今
来描述,从C点走到今天的D点,是震荡筑底阶段,而今 天出现了明显的
天出现了明显的 筑底结束的标志,且D点和C
筑底结束的标志,且D点和C 点正
点正 好关于直线
好关于直线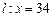 对称。老赵预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线
对称。老赵预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线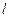 对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。现在老赵决定取点
对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。现在老赵决定取点 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得 。
。
(1)请你帮老赵算出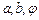
 ,并回答股价什么时候见顶(即求F点的横坐标);
,并回答股价什么时候见顶(即求F点的横坐标);
(2)老赵如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
(本小题满分12分)
设向量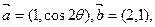
 ,其中
,其中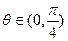 .
.
(1)求 的取值范围;
的取值范围;
(2)若函数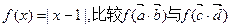 的大小
的大小
(本小题满分12分)
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ )的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若
)的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若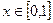 ,求函数y=2sin(πx+φ)的最值,及取得最值时
,求函数y=2sin(πx+φ)的最值,及取得最值时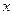 的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求
的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求 的余弦值。
的余弦值。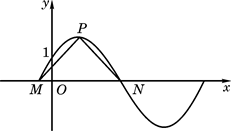
(本小题满分12分)
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)完成频率分布表;
| 分组 |
频数 |
频率 |
| 100~200 |
||
| 200~300 |
||
| 300~400 |
||
| 400~500 |
||
| 500~600 |
||
| 合计 |
(2)画出频率分布直方图和频率分布折线图;
(3)估计电子元件寿命在100~400小时以内的频率;