已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤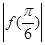 对x∈R恒成立,且
对x∈R恒成立,且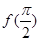 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
A.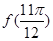 =-1 =-1 |
B.f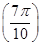 >f >f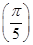 |
| C.f(x)是奇函数 |
D.f(x)的单调递增区间是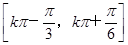 (k∈Z) (k∈Z) |
将函数y=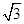 cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
A. |
B.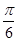 |
C.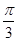 |
D.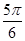 |
已知函数f(x)=2sin(ωx+φ)(ω>0)的图象关于直线x=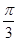 对称,且f
对称,且f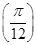 =0,则ω的最小值为( ).
=0,则ω的最小值为( ).
| A.2 | B.4 | C.6 | D.8 |
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ= ”的( ).
”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
将函数y=sin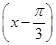 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为( ).
个单位,则所得函数图象对应的解析式为( ).
A.y=sin |
B.y=sin |
C.y=sin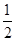 x x |
D.y=sin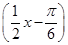 |