人造地球卫星绕地球旋转时，既具有动能又具有引力势能（引力势能实际上是卫星与地球共有的，简略地说此势能是人造卫星所具有的）.设地球的质量为M，以卫星离地还需无限远处时的引力势能为零，则质量为m的人造卫星在距离地心为r处时的引力势能为EP=-GMm/r（G为万有引力常量）. 当物体在地球表面的速度等于或大于某一速度时，物体就可以挣脱地球引力的束缚，成为绕太阳运动的人造卫星，这个速度叫做第二宇宙速度.用R表示地球的半径，M表示地球的质量，G表示万有引力常量.试写出第二宇宙速度的表达式.
．为了测量某住宅大楼每层的平均高度（层高）及电梯运行情况，甲、乙两位同学在一楼电梯内用压力传感器进行了如下实验:甲同学站在压力传感器上，乙同学负责观察电梯从地面一楼到顶层全过程中，压力传感器示数随时间变化的情况。如图所示是压力传感器示数随时间变化图，已知t=0时，电梯静止不动，电梯共上升18层的高度。求：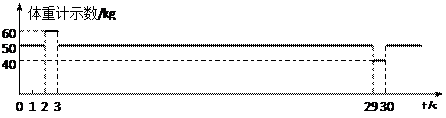
（1）电梯启动和制动时的加速度大小；
（2）该大楼的层高(设每层高度相同)。
如图所示，吊篮A、物体B、物体C的质量相等，弹簧质量不计，B和C分别固定在弹簧两端，放在吊篮的水平底板上静止不动。将悬挂吊篮的轻绳剪断的瞬间B、C的加速度各是多大？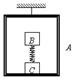
设雨点下落过程受到的空气阻力与雨点的横截面积S成正比，与雨点下落的速度v的平方成正比，即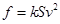
（其中k为比例系数）．雨点接近地面时近似看做匀速直线运动，重力加速度为g．若把雨点看做球形，其半径为r,球的体积为
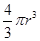，设雨点的密度为
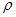，求：
(1)每个雨点最终的运动速度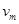
（用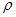、r、g、k表示）；
(2)雨点的速度达到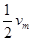
时，雨点的加速度a为多大？
有一种简单夯锤结构如图所示，打夯时共有5人，四个人分别握住夯锤的一个把手，一个人负责喊号，喊号人一声号子，四人同时向上发力将夯锤提起，号音一落四人同时松手，夯锤落至地面将地基夯砸实。某次打夯时，设夯锤的质量为80kg，将夯锤提起时，每个人都对夯锤施加竖直向上的力，大小均为250N，力的持续时间为0.6s，然后松手。夯锤落地时将地面砸出2cm深的一个凹痕。求：
（1）夯锤能够上升的最大高度？
（2）夯锤落地时对地面的平均作用力为多大？（g=10m/s2）
一定质量的理想气体由状态A经状态B变为状态C，其中A
B过程为等压变化，BC过程为等容变化。已知VA=0.3m3，TA=TB=300K、TB=400K。
（1）求气体在状态B时的体积。
（2）说明BC过程压强变化的微观原因
（3）没AB过程气体吸收热量为Q，BC过 气体放出热量为Q2，比较Q1、Q2的大小说明原因。