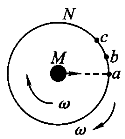
如图所示,M、N是两个共轴圆筒横截面,外筒半径为R,内筒半径比R小得多,可以忽略不计,筒的两端是封闭的,两筒之间抽成真空,两筒以相同的角速度ω绕其中心轴线(图中垂直于纸面)作匀速转动。设从M筒内部可以通过狭缝s(与M筒的轴线平行)不断地向外射出两种不同速率v1和v2的微粒,从s处射出时的初速度的方向都是沿筒的半径方向,微粒到达N筒后就附着在N筒上.如果R、v1和v2都不变,而ω取某一合适的值,则( )
| A.有可能使微粒落在Ⅳ筒上的位置都在a处一条与s缝平行的窄条上 |
| B.有可能使微粒落在N筒上的位置都在某处,如b处一条与缝s平行的窄条上 |
| C.有可能使微粒落在N筒上的位置分别在某两处,如b处和c处与s缝平行的窄条上 |
| D.只要时间足够长,N筒上到处都落微粒 |
下列说法正确的是( )
| A.参考系必须是固定不动的物体 |
| B.参考系可以是变速运动的物体 |
| C.地球很大,又因有自转,研究地球公转时,地球不可视为质点 |
| D.研究跳水运动员转体动作时,运动员可视为质点 |
关于分子动理论,下列说法中错误的是
| A.显微镜下观察到墨水中的小碳粒在不停的作无规则运动,这反映了液体分子运动的无规则性 |
| B.随着分子间距离的增大,分子间的相互作用力一定先减小后增大 |
| C.随着分子间距离的增大,分子势能可能先减小后增大 |
| D.在真空、高温条件下,可以利用分子扩散向半导体材料掺入其他元素 |
如图所示,物体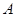 、
、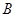 的质量相等,物体
的质量相等,物体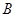 刚好与地面接触. 现剪断绳子
刚好与地面接触. 现剪断绳子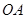 ,下列说法正确的是
,下列说法正确的是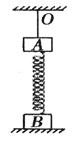
A.剪断绳子的瞬间,物体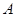 的加速度为 的加速度为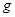 |
B.弹簧恢复原长时,物体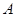 的速度最大 的速度最大 |
C.弹簧压缩到最短时,物体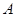 的加速度为0 的加速度为0 |
D.剪断绳子后,弹簧、物体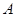 、 、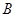 和地球组成的系统机械能守恒 和地球组成的系统机械能守恒 |
如图所示是某公园设计的一种惊险刺激的娱乐设施. 管道除 点右侧水平部分粗糙外,其余部分均光滑. 若挑战者自斜管上足够高的位置滑下,将无能量损失的连续滑入第一个、第二个圆管形管道
点右侧水平部分粗糙外,其余部分均光滑. 若挑战者自斜管上足够高的位置滑下,将无能量损失的连续滑入第一个、第二个圆管形管道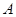 、
、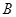 内部(圆管
内部(圆管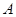 比圆管
比圆管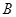 高).某次一挑战者自斜管上某处滑下,经过第一个圆管形管道
高).某次一挑战者自斜管上某处滑下,经过第一个圆管形管道 内部最高位置时,对管壁恰好无压力.则这名挑战者
内部最高位置时,对管壁恰好无压力.则这名挑战者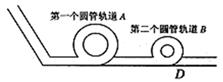
A.经过管道 最高点时的机械能大于经过管道 最高点时的机械能大于经过管道 最低点时的机械能 最低点时的机械能 |
B.经过管道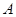 最高点时的动能大于经过管道 最高点时的动能大于经过管道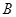 最低点时的动能 最低点时的动能 |
C.经过管道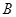 最高点时对管外侧壁有压力 最高点时对管外侧壁有压力 |
D.不能经过管道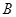 的最高点 的最高点 |
如图所示,一位飞行员驾驶着一架飞机在竖直面内沿环线做匀速圆周飞行.飞机在环线最顶端完全倒挂的瞬间,飞行员自由的坐在座椅上,对安全带和座椅没有任何力的作用,则下列说法正确的是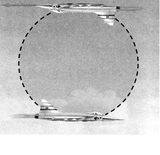
| A.飞机在环线最顶端的瞬间,飞行员处于失重状态 |
| B.飞机在环线最底端的瞬间,飞行员处于失重状态 |
| C.飞机在环线最左端的瞬间,飞行员处于平衡状态 |
| D.飞机在环线最底端的瞬间,飞行员处于平衡状态 |