已知物体从地球上的逃逸速度(第二宇宙速度) ,其中G、ME、RE分别是引力常量、地球的质量和半径。已知G=6.7×10-11N·m2/kg2,c=3.0×108m/s,求下列问题:(1)逃逸速度大于真空中光速的天体叫做黑洞,设某黑洞的质量等于太阳的质量M=2.0×1030kg,求它的可能最大半径(这个半径叫Schwarhid半径);(2)在目前天文观测范围内,物质的平均密度为10-27kg/m3,如果认为我们的宇宙是这样一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的速度c,因此任何物体都不能脱离宇宙,问宇宙的半径至少多大?(最后结果保留两位有效数字)
,其中G、ME、RE分别是引力常量、地球的质量和半径。已知G=6.7×10-11N·m2/kg2,c=3.0×108m/s,求下列问题:(1)逃逸速度大于真空中光速的天体叫做黑洞,设某黑洞的质量等于太阳的质量M=2.0×1030kg,求它的可能最大半径(这个半径叫Schwarhid半径);(2)在目前天文观测范围内,物质的平均密度为10-27kg/m3,如果认为我们的宇宙是这样一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的速度c,因此任何物体都不能脱离宇宙,问宇宙的半径至少多大?(最后结果保留两位有效数字)
一位质量为60kg的运动员,用12s时间跑完100m,设他在运动过程中受到的阻力保持不变,并且他在开始运动的前2s时间内作匀加速直线运动,后面10s时间内则保持他在第2s末时的瞬时功率值不变,继续作直线运动,最后一段时间作的是匀速运动。已知他在作匀速运动时的速度大小是11m/s。求
①他在跑这100m的过程中,平均功率多大?
②他在运动过程中受到的阻力多大?
两块厚度不同的木板并在一起,直立固定在地面上。一颗子弹水平射向木板,恰好把这两块木板射穿。已知它通过这两块木板所用时间之比为1:2,并且子弹通过这两块木板时受到的阻力大小相等,求这两块木板的厚度之比。

如图所示,质量为1kg的物块放在粗糙的水平地面上,物块与地面间动摩擦因数μ=0.1。物块左侧连接弹簧,弹簧另一端固定在竖直墙上,构成一个弹簧振子。现在把物块拉至平衡位置右侧10cm处作为初始位置,把物块从初始位置由静止释放。当物块第一次通过平衡位置左侧5cm处时的速度v=1m/s。g取10m/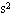 。求
。求
(1)这一过程中物块动能的变化量。
(2)这一过程,弹簧弹力所做的功。
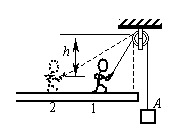
如图所示,一人站在一平台上,拉动绕过定滑轮的绳子使重物上升。已知重物重为400N,绳的重量及滑轮的摩擦均可忽略不计。他手握住绳端,从位置1(绳与竖直方向成30°角)缓慢移动到位置2(绳与竖直方向成60°角),已知绳端距定滑轮的高度h=2.0m。他在这个过程中,拉绳端的力做了多少功?
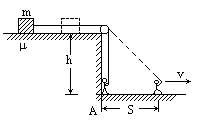
如图,在高h的平台上,放有一质量为m的物体,一根系住物体的绳子绕过定滑轮被站在高台下的人拉住.该人从A处由静止开始拉着绳子向右运动,前进距离s时人的速度为ν.若人的高度、滑轮的大小及摩擦均不计,求这一过程中绳的拉力对物体做的功.