如图13-1所示,物体A从高h的P处沿光滑曲面从静止开始下滑,物体B用长为L的细绳竖直悬挂在O点且刚和平面上Q点接触。已知mA=mB,高h及S(平面部分长)。若A和B碰撞时无能量损失。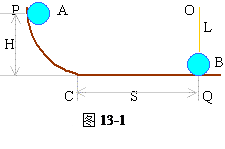
(1)若L≤h/4,碰后A、B各将做什么运动?
(2)若L=h,且A与平面的动摩擦因数为μ,A、B可能碰撞几次?A最终在何处?
如图8-4-9所示,在光滑水平面上两平板车的质量分别为M1="2" kg和M2="3" kg,在M1的光滑表面上放有质量m="1" kg的滑块,与M1一起以5 m/s速度向右运动,M1与M2相撞后以相同的速度一起运动,但未连接,最后m滑上M2,因摩擦而停在M2上.求最终M1、M2的速度.
图8-4-9
一辆装有砂子的小车,总质量M="10" kg,以速度v0="2" m/s沿光滑水平直轨运动.有一质量m="2" kg的铁球以速度v="7" m/s投入小车内的砂子中,求下列各种情况下,铁球投入后小车的速度.
(1)铁球迎面水平投入;
(2)铁球从后面沿车行方向投入;
(3)铁球由小车上方竖直向下投入.
如图所示,质量均为m的A、B两个弹性小球,用长为2 l的不可伸长的轻绳连接。现把A、B两球置于距地面高H处(H足够大),间距为l当A球自由下落的同时,B球以速度v0指向A球水平抛出。求: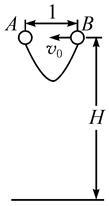
(1)两球从开始运动到相碰,A球下落的高度。
(2)A、B两球碰撞(碰撞时无机械能损失)后,各自速度的水平分量。
(3)轻绳拉直过程中,B球受到绳子拉力的冲量大小。
如图7所示,甲、乙两个小孩各乘一辆冰车在水平冰面上游戏,甲和他的冰车总质量为M="30" kg,乙和他的冰车总质量也是30 kg.游戏时,甲推着一个质量m="15" kg的箱子,和他一起以大小为v0="2" m/s的速度滑行,乙以同样大小的速度迎面滑来.为了避免相撞,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住.若不计冰面的摩擦,则甲至少要以__________的速度(相对地面)将箱子推出,才能避免与乙相撞.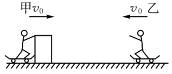
图7
在光滑水平桌面上,有一长为l="2" m的木板C,它的两端各有一挡板,C的质量mC="5" kg,在C的正中央并排放着两个可视为质点的滑块A、B,质量分别为mA="1" kg,mB="4" kg,开始时A、B、C都静止,并且AB间夹有少量的塑胶炸药,如图16-5-2所示,炸药爆炸使得A以6 m/s的速度水平向左运动,如果A、B与C间的摩擦可忽略不计,两滑块中任一块与挡板碰撞后都与挡板结合成一体,爆炸和碰撞时间都可忽略.求:
图16-5-2
(1)当两滑块都与挡板相撞后,板C的速度多大?
(2)到两个滑块都与挡板碰撞为止,板的位移大小和方向如何?