用一根长l的细线,一端固定在顶板上,另一端拴一个质量为m的小球.现使细线偏离竖直方向α角后,从A处无初速地释放小球(图4-21).试问:
(1)小球摆到最低点O时的速度?
(2)小球摆到左方最高点的高度(相对最低点)?
向左摆动过程中能达到的最大高度有何变化?
如图,圆柱形筒,底面直径为d,观察者沿筒的边缘可看到筒壁h深处的M点.当筒内装满某种液体时,观察者沿筒的边缘可看到筒壁H深处的N点,则这种液体的折射率n多大?.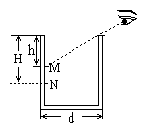
(1)汽车在整个运动过程中所能达到的最大速度;
(2)匀加速运动能保持多长时间;
(3)当汽车的速度为5m/s时的瞬时功率;
(4)当汽车的速度为8m/s时的加速度。
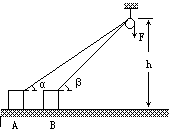
用拉力F=120N竖直向下拉绳,通过定滑轮使质量m=5kg的物体从位置A移到位置B,已知在A、B两位置时,绳与水平方向间的夹角α=30°,β=37°,高度h=2m,如图所示,不计绳子质量和滑轮的摩擦,则人在这个过程中的拉力做了多少功?(sin37°=0.6,cos37°=0.8)