将边长为a的正方形沿对角线AC折起,使得BD=a,则三棱锥D﹣ABC的体积为()
| A.6a3 | B.12a3 | C.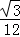 a3 a3 |
D.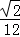 a3 a3 |
对于直线m、n和平面α,下面命题中的真命题是()
| A.如果m⊂α,n⊄α,m、n是异面直线,那么n∥α |
| B.如果m⊂α,n与α相交,那么m、n是异面直线 |
| C.如果m⊂α,n∥α,m、n共面,那么m∥n |
| D.如果m∥α,n∥α,m、n共面,那么m∥n |
将正方体的纸盒展开如图,直线AB、CD在原正方体的位置关系是()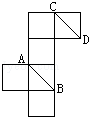
A.平行
B.垂直
C.相交成60°角
D.异面且成60°角
已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()
| A.16π | B.20π | C.24π | D.32π |
平行六面体ABCD﹣A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为()
| A.3 | B.4 | C.5 | D.6 |