如图1,在直角梯形 中,
中,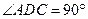 ,
, ,
,
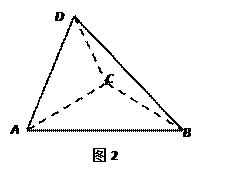

 .将
.将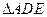 沿
沿 折起,使平面
折起,使平面
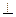 平面
平面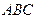 ,得到几何体
,得到几何体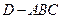 ,如图2所示.(Ⅰ) 求证:
,如图2所示.(Ⅰ) 求证: 平面
平面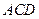 ;(Ⅱ) 求几何体
;(Ⅱ) 求几何体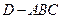 的体积.
的体积.

有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
20 |
||
| 乙班 |
60 |
||
| 总计 |
210 |
已知从全部210人中随机抽取1人为优秀的概率为 .
.
(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附: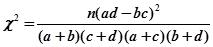 ,其中
,其中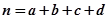 .
.
| 参考数据 |
当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; |
|
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; |
|
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设 为取得红球的个数.
为取得红球的个数.
(1)求 的分布列;
的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
证明:在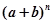 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
已知函数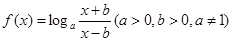 .
.
(1)求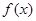 的定义域;
的定义域;
(2)讨论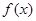 的奇偶性;
的奇偶性;
(3)讨论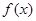 的单调性.
的单调性.
已知函数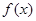 ,当
,当 时,恒有
时,恒有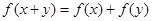 .
.
(1)求证: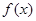 是奇函数;
是奇函数;
(2)如果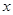 为正实数,
为正实数, ,并且
,并且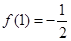 ,试求
,试求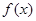 在区间[-2,6]上的最值.
在区间[-2,6]上的最值.