水平向上足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接;导轨上放一质量为m的金属杆(如图12-2-21所示),金属杆与导轨的电阻忽略不计;均匀磁场竖直向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力大小时,相对应的匀速运动速度 也会变化,
也会变化, 和F的关系如图12-2-22所示.(取重力加速度
和F的关系如图12-2-22所示.(取重力加速度 )
)
(1)金属杆在匀速运动之前做什么运动?
(2)若 ,
, ,
, ;磁感应强度B为多大?
;磁感应强度B为多大?
(3)由 -F图线的截距可求得什么物理量?其值为多少?
-F图线的截距可求得什么物理量?其值为多少?
如图2-8(原图2-11)所示,一个带滑轮的物体放在水平面上,一根轻绳固定在C处,通过滑轮B和D牵引物体,BC水平,以水平恒速v拉绳上自由端时,物体沿水平面前进.求当跨过B的两绳夹角为时,物体的运动速度为多少?[10]
如图2-6(原图2-10)所示,一辆实验小车可沿水平地面(图中纸面)上的长直轨道匀速向右运动.有一台发出细激光束的激光器装在小转台M上,到轨道的距离MN为d = 10m,转台匀速转动,使激光束在水平面内扫描,扫描一周的时间为T = 60s.光束转动方向如图中箭头所示.当光束与MN的夹角为45°时,光束正好射到小车上.如果再经过△t = 2.5s光束又射到小车上,则小车的速度为多少?(结果保留两位数字) [8]
轮船在河流中逆流而上,下午7时,船员发现轮船上的一橡皮艇已失落水中,船长命令马上掉转船头寻找小艇.经过一个小时的追寻,终于追上了顺流而下的小艇.如果轮船在整个过程中相对水的速度不变,那么轮船失落小艇的时间是何时?[3 ]
甲乙两地相距220km,A车用40km/h的速度由甲地向乙地匀速运动,B车用30km/h的速度由乙地向甲地匀速运动.两车同时出发,B车出发后1h,在途中暂停2h后再以原速度继续前进,求两车相遇的时间和地点.[3 ]
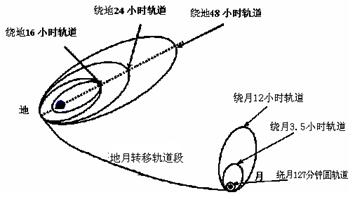
如下图是我国“嫦娥一号”发射及绕月简图,设下图中卫星是逆时针方向运动的,阅读如下材料回答下面问题:
2007年10月25日17时55分,北京航天飞行控制中心对嫦娥一号卫星实施首次变轨并获得成功,首次变轨是在远地点发动机点火使卫星加速的。卫星的近地点高度由约200公里抬高到了约600公里,如图卫星正式进入绕地16小时轨道。接下来卫星在近地点处还要借助自身发动机的推动经过三次变轨即进入绕地24小时轨道、绕地48小时轨道,最后进入地月转移轨道经过漫长的施行后接近月球,在月球近月点的位置仍要借助自身的发动机的作用,使卫星的速度发生变化,被月球引力俘获后进入绕月12小时轨道、绕月3.5小时轨道,最终进入绕月127分钟的圆形轨道,进行约一年的月球探索之旅。
“嫦娥一号”卫星最终是以127分钟的周期T稳定运行于月球的圆周轨道上,若已知地球的质量是月球m质量81倍,地球半径是月球半径r的3.7倍,试用引力常量G、m、T、r写出卫星距月球表面的高度H的表达式。
若已知地球的质量 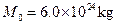 ,地球的半径
,地球的半径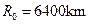 ,万有引力恒量
,万有引力恒量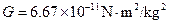 ,试结合给出的数据,求出H的数值。(保留两位有效数字)
,试结合给出的数据,求出H的数值。(保留两位有效数字)