(本小题满分13分)已知数列 中,
中, ,数列
,数列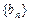 中,
中, .(Ⅰ)求数列
.(Ⅰ)求数列 通项公式;(Ⅱ)求数列
通项公式;(Ⅱ)求数列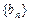 通项公式以及前
通项公式以及前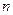 项的和.
项的和.
(本小题满分12分)如图所示,正方体ABCD-A1B1C1D1中,P、Q分别是AD1、BD上的点,且AP=BQ,求证:PQ∥平面DCC1D1.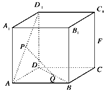
(本小题满分12分)如图所示,已知A(1,3),B(-1,-1),C(2,1).求△ABC的BC边上的高所在的直线方程.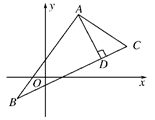
(本小题满分12分)已知圆
 与
与 轴相切.
轴相切.
(1)求 的值;
的值;
(2)若圆 的切线在
的切线在 轴和
轴和 轴上的截距相等,求该切线方程;
轴上的截距相等,求该切线方程;
(3)从圆外一点 向圆引切线,M为切点,O为坐标原点,且有
向圆引切线,M为切点,O为坐标原点,且有 ,求使
,求使 最小的点P的坐标.
最小的点P的坐标.
(本小题满分12分)已知关于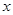 的不等式
的不等式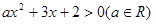
(1)若不等式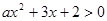 的解集为
的解集为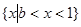 ,求
,求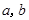 的值.
的值.
(2)求关于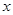 的不等式
的不等式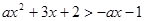
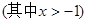 的解集
的解集
(本小题满分12分)如图所示,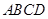 是正方形,
是正方形,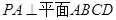 ,
,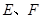 是
是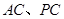 的中点.
的中点.
(1)求证: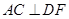 ;
;
(2)若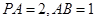 ,求三棱锥
,求三棱锥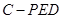 的体积.
的体积.