(本小题满分14分)
已知等比数列{an}中,a2=32,a8=,an+1<an
(1)求数列{an}的通项公式;
(2)设Tn=log2a1+log2a2+…+log2an,求Tn的最大值及相应的n值
已知函数 的图象为曲线E.
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数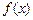 可以在
可以在 和
和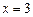 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(Ⅲ) 在满足(2)的条件下,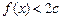 在
在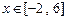 恒成立,求c的取值范围.
恒成立,求c的取值范围.
函数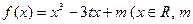 和
和 为实常数)是奇函数,设
为实常数)是奇函数,设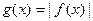 在
在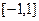 上的最大值为
上的最大值为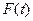 . ⑴求
. ⑴求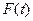 的表达式; ⑵求
的表达式; ⑵求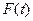 的最小值.
的最小值.
已知函数 的图象过原点,
的图象过原点,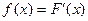 ,
, ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
(1)若y=F(x)在x=-1处取得极大值2,求函数y=F(x)的单调区间;
(2)若使g(x)=0的x值满足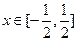 ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围;
已知函数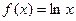
(1)求函数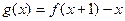 的最大值;
的最大值;
(2)当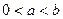 时,求证
时,求证 ;
;
函数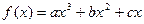 (
(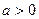 )的图象关于原点对称,
)的图象关于原点对称, 、
、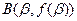 分别为函数
分别为函数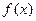 的极大值点和极小值点,且|AB|=2,
的极大值点和极小值点,且|AB|=2,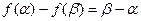 .
.
(Ⅰ)求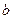 的值;
的值;
(Ⅱ)求函数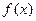 的解析式;
的解析式;
(Ⅲ)若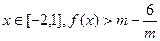 恒成立,求实数
恒成立,求实数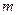 的取值范围.
的取值范围.