有一倾角为θ的斜面，其底端固定一挡板M，另有三个木块A、B和C，它们的质
量分别为m
=m
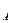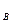=m，m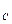
="3" m，它们与斜面间的动摩擦因数都相同.其中木块A连接一轻弹簧放于斜面上，并通过轻弹簧与挡板M相连，如图所示.开始时，木块A静止在P处，弹簧处于自然伸长状态.木块B在Q点以初速度v
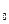向下运动，P、Q间的距离为L.已知木块B在下滑过程中做匀速直线运动，与木块A相碰后立刻一起向下运动，但不粘连，它们到达一个最低点后又向上运动，木块B向上运动恰好能回到Q点.若木块A静止于P点，木块C从Q点开始以初速度
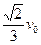向下运动，经历同样过程，最后木块C停在斜面上的R点，求P、R间的距离L′的大小。
一辆质量为M的汽车，后面挂一节质量为m的拖车，在恒定的牵引力作用下从静止开始以加速度a作匀加速直线运动，通过位移S时，汽车与拖车脱钩，此后汽车所受牵引力和两车所受摩擦力均不变，又经过时间t拖车停止运动，求此时汽车的速度多大?
在一个很大的水平台面上靠在一起放有两静止的木块A和B，A和B的质量都是100g，今有一颗质量为10g的子弹以某一水平速度飞来先后射穿A和B后, A和B都在水平面上发生了滑动, 并且最后又都静止下来．已知当B刚好停下来时，它与A相距0.8m，与子弹相距23.1m．设子弹在穿越A和穿越B时所受到的阻力相等，所用的时间也相等，木块与水平台面间的动摩擦因数均为0.5，且木块很小，因而计算中可以忽略木块本身的大小和子弹穿越木块的极短时间内木块的位移，取g=10m/
，求：
(1)A由滑动而刚好停下来时，A与B相距多远?
(2)A由滑动而刚好停下来时，A与子弹相距多远?
(3)子弹刚射穿A时，子弹的速度为多大?
质量为M的金属球与质量为m的木球用细线相连，没入水中，细线竖直绷直．两球从静止开始以加速度a在水中下沉．经过时间t细线断了，球分开，再经过时间
，木球停止下沉，求此时金属球的速度！（在运动过程中水的阻力不计）
如图所示，长1.8m的细线下悬挂着质量为2kg的小球，开始时球离地面3.6m高，现将小球送到悬挂处放手后，让球自由落下，此小球在原静止位置A处绷断悬线落地．已知小球从自由落下到着地所经历的全部时间为1.2s，g=10m/
，求细线断裂时小球所受到的合冲量是多少？