矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影A′落在BC上,求二面角A-BD-C的大小的余弦值.
将背面相同正面分别标有1、2、3、4的四张卡片洗匀后背面朝上放在桌面上,(1)从中随机的抽取一张卡片,求该卡片正面上的数字是偶数的概率(2)先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?
设正有理数x是 的一个近似值,令
的一个近似值,令 。
。
(Ⅰ)若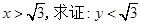 ;
;
(Ⅱ)比较y与x哪一个更接近于 ,请说明理由.
,请说明理由.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于点D,过B作圆O的切线交AD的延长线于E.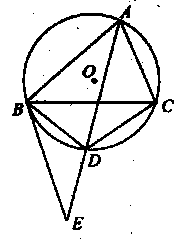
(Ⅰ)求证:∠EBD=∠CBD;
(II)求证:AB·DE=CD·BE.
已知函数 在点
在点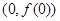 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+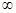 )均有
)均有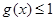 恒成立.
恒成立.
(Ⅰ)求a,b,c的值;
(Ⅱ)求证: 。
。
在平面直角坐标系中,已知定点A(-2,0)、B(2,0),异于A、B两点的动点P满足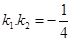 ,其中k1、k2分别表示直线AP、BP的斜率.
,其中k1、k2分别表示直线AP、BP的斜率.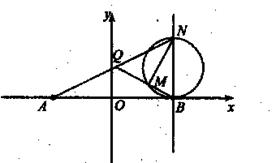
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若N是直线x=2上异于点B的任意一点,直线AN与(I)中轨迹E交予点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),点C(1,0),求证:|CM|·|CN|为定值.