一个质点正在作匀加速度速直线运动,用固定在地面上的照相机对该质点进行闪光照相,闪光时间间隔为1s。分析照片得到的数据,发现质点在第1次、第2次闪光的时间间隔内移动了2m;在第3次、第4次闪光的时间间隔内移动了8m。由此可以求得( )
| A.第1次闪光时质点的速度 |
| B.质点运动的加速度 |
| C.从第2次闪光到第3次闪光这段时间内质点的位移 |
| D.质点运动的初速度 |
如图所示为洗衣机脱水筒的示意图,当脱水筒从静止开始到完成脱水的过程中
| A.衣服始终做离心运动 | B.衣服始终做匀速圆周运动 |
| C.衣服上有水做离心运动 | D.衣服上的水始终做匀速圆周运动 |
如图所示,一个用细绳系着的橡皮塞在水平面内做匀速圆周运动,此橡皮塞
| A.只受重力 | B.只受绳的拉力 |
| C.受重力和绳的拉力 | D.受重力、绳的拉力和向心力 |
如图所示,水平桌面上有一弯曲的轨道,钢球以一定的速度从轨道的始端进入,末端离开。对钢球在轨道末端速度方向的判断,图中表示正确的是
A. |
B. |
C. |
D. |
有两个共点力,一个力的大小是3 N,另一个力的大小是6 N,它们合力的大小可能是
| A.18 N | B.9 N | C.2 N | D.1 N |
如图所示,长为0.8m的细线一端固定于O点,另一端系一小球。将细线拉至水平后由静止释放小球,当小球经过最低点时的速度大小为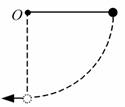
A.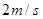 |
B.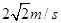 |
C.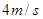 |
D.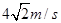 |