
在同一平台上的O点抛出的3个物体,做平抛运动的轨迹均在纸面内,如图所示,则3个物体做平抛运动的初速度 的关系及落地时间
的关系及落地时间 的关系分别是( )
的关系分别是( )
A.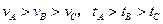 |
B.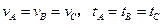 |
C.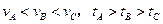 |
D.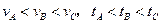 |

如图所示,MN、PQ是两根足够长的固定的平行金属杆,导轨间距L,导轨平面与水平夹角θ,整个导轨平面处于一个垂直平面向上的匀强磁场B,PM间有一电阻R,一金属杆ab质量m,从静止沿光滑导轨下滑,导轨与金属杆电阻不计。
(1)ab杆下滑瞬间的加速度是多大。
(2)ab哪端电势高。
(3)杆的最大速度是多大。

如图所示,正方形线框边长L,质量M,电阻R,从高H处自由下落,当线框的下边进入高h =" L" 的有界匀强磁场时,恰好匀速下降,设线框面总与磁场垂直,求
(1)磁感应强度B
(2)线框经过磁场过程中所产生热Q
(3)线框穿过该区域共需时间T

一列横波在t=0时刻的波形如图,传播方向沿x轴正方向,已知在0.9s末,P点恰好出现第3次波谷,则从零时刻算起,经过多长时间,在Q点第1次出现波峰?
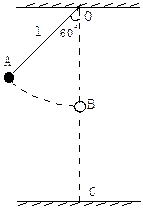
如图,让质量m=5kg的摆球由图中所示位置A从静止开始下摆。摆至最低点B点时恰好绳被拉断。设摆线长 =1.6m,悬点O与地面的距离OC=4m,若空气阻力不计,绳被拉断瞬间小球的机械能无损失。(g=10m/s2)
=1.6m,悬点O与地面的距离OC=4m,若空气阻力不计,绳被拉断瞬间小球的机械能无损失。(g=10m/s2)
求:(1)绳子所能承受的最大拉力T
(2)摆球落地的速率v
一列简谐横波沿直线传播,在波的传播方向上有P、Q两个质点,它们相距0.8m。当t=0时,P、Q两点的位移恰好是正最大值,且P、Q间只有一个波谷。当t=0.6s时,P、Q两点正好处于平衡位置,且P、Q两点只有一个波峰和一个波谷,且波峰距Q点的距离第一次为0.2m。求:
(1)波由P传至Q,波的周期。
(2)波由Q传至P,波的速度。
(3)波由Q传至P,从t=0时开始观察,哪些时刻P、Q间(P、Q除外)只有一个质点的位移等于振幅。