某游乐场中有一种叫“空中飞椅”的游乐设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋。若将人和座椅看成是一个质点,则可简化为如图所示的物理模型。其中P为处于水平面内的转盘,可绕竖直转轴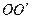 转动,设绳长l="10" m,质点的质量m= 60kg,转盘静止时质点与转轴之间的距离d =4m。转盘逐渐加速转动,经过一段时间后质点与转盘一起做匀速圆周运动,此时绳与竖直方向的夹角
转动,设绳长l="10" m,质点的质量m= 60kg,转盘静止时质点与转轴之间的距离d =4m。转盘逐渐加速转动,经过一段时间后质点与转盘一起做匀速圆周运动,此时绳与竖直方向的夹角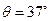 。(不计空气阻力及绳重,绳子不可伸长,sin
。(不计空气阻力及绳重,绳子不可伸长,sin 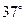 ="0." 6,cos
="0." 6,cos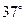 ="0." 8,g=10
="0." 8,g=10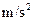 )求:
)求:
(1)质点与转盘一起做匀速圆周运动时转盘的角速度及绳子的拉力;
(2)质点从静止到做匀速圆周运动的过程中,绳子对质点做的功。
某发电站的输出功率为104 kW,输出电压为4 kV,通过理想变压器升压后向80 km远处用户供电.已知输电线的电阻率为ρ=2.4×10-8 Ω·m,导线横截面积为1.5×10-4 m2,输电线路损失的功率为输出功率的4%,求:
(1)升压变压器的输出电压;
(2)输电线路上的电压损失.
某电厂要将电能输送到较远的用户,输送的总功率为9.8×104 W,电厂输出电压仅为350 V,为减少输送功率损失,先用一升压变压器将电压升高再输出,已知输电线路的总电阻为4 Ω,允许损失的功率为输送功率的5%,所需电压为220 V,求升压、降压变压器的原副线圈的匝数比各是多少.
如图13-1-3所示,边长为a的单匝正方形线圈在磁感应强度为B的匀强磁场中,以OO′边为轴匀速运动,角速度为ω,转轴与磁场方向垂直,线圈电阻为R.求:
图13-1-3
(1)线圈从图示位置转过90°的过程中产生的热量;
(2)线圈从图示位置转过90°的过程中通过线圈某截面的电荷量q.
某水利发电站采用高压输电将电能输送到华北地区,输送电路如图13-26所示,升压、降压变压器均为理想变压器.输送的总电功率为P=4.5×106 kW.发电机输出的电压为U0="18" kV.输电电压为U="500" kV.要使输电线上损耗的功率等于输电功率的5%.求: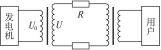
图13-26
(1)发电站的升压变压器原、副线圈的匝数比;
(2)输电线路的总电阻R.
如图13-35(甲)所示,一固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平均数垂直的均匀分布的磁场.已知线圈的匝数n=100匝,电阻r="1.0" Ω,所围成矩形的面积S="0.040" m2,小灯泡的电阻R="9.0" Ω,磁感应强度随时间按如图13-35(乙)所示的规律变化,线圈中产生的感应电动势瞬时值的表达式为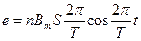 ,其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求:
,其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求: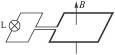
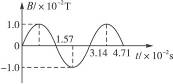
(甲)(乙)
图13-35
(1)线圈中产生感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的0—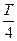 的时间内,通过小灯泡的电荷量.
的时间内,通过小灯泡的电荷量.