已知函数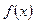 与函数
与函数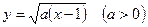 的图像关于直线
的图像关于直线 对称.
对称.
(1)试用含 的代数式表示函数
的代数式表示函数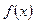 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列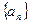 中,
中,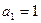 ,当
,当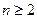 时,
时, .数列
.数列 中,
中,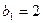 ,
,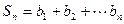 .点
.点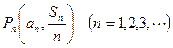 在函数
在函数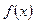 的图像上,求
的图像上,求 的值;
的值;
(3)在(2)的条件下,过点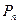 作倾斜角为
作倾斜角为 的直线
的直线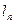 ,则
,则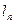 在y轴上的截距为
在y轴上的截距为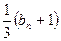
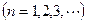 ,求数列
,求数列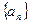 的通项公式.
的通项公式.
某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,得到成绩分布的频率分布直方图如图:
(1)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(2)将上述调查所得到的频率视为概率.现在从该校大量高一学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的合格人数为 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求 的分布列和期望
的分布列和期望 ;
;
| 高一 |
高二 |
合计 |
|
| 合格人数 |
|||
| 不合格人数 |
|||
| 合计 |
(3)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写2×2列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系” .
一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
| P |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求 的分布列及期望
的分布列及期望 .
.
在各项为正的数列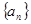 中,数列的前n项和
中,数列的前n项和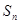 满足
满足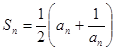 ,
,
(1)求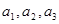 ;
;
(2)由(1)猜想数列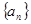 的通项公式;
的通项公式;
(3)求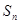
已知不等式
(1)若对于所有的实数 不等式恒成立,求
不等式恒成立,求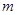 的取值范围;
的取值范围;
(2)设不等式对于满足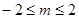 的一切
的一切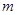 的值都成立,求
的值都成立,求 的取值范围
的取值范围
(本小题满分14分)如图,在四棱锥 中,
中,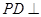 平面
平面 ;四边形
;四边形 是菱形,经过
是菱形,经过 作与
作与 平行的平面交
平行的平面交 与点
与点 ,
, 的两对角线交点为
的两对角线交点为 .
.
求证: ;
;