如图所示,两个带电小球A、B用长度为L=10cm的细丝线相连放在光滑绝缘水平面上保持静止。已知这时细丝线对B球的拉力大小F0=1.8×10-2N, A球的电荷量为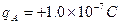 ,
,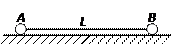
求:小球A所受的电场力F的大小。
小球B的电性和电荷量qB。(静电力常量k=9.0×109Nm2/C2)
如图所示,热电子由阴极飞出时的初速忽略不计,电子发射装置的加速电压为U0。电容器板长和板间距离均为L=10cm,下极板接地。电容器右端到荧光屏的距离也是L=10cm。在电容器两极板间接一交变电压,上极板的电势随时间变化的图象如左图。(每个电子穿过平行板的时间极短,可以认为电压是不变的)求:

①在t=0.06s时刻,电子打在荧光屏上的何处
②荧光屏上有电子打到的区间有多长?
③屏上的亮点如何移动?
如图所示,真空中相距d="5" cm的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图所示.将一个质量 ,电量
,电量 的带电粒子从紧临B板处释放,不计重力.求:
的带电粒子从紧临B板处释放,不计重力.求:

(1)在t=0时刻释放该带电粒子,释放瞬间粒子加速度的大小;
(2)若A板电势变化周期 ,在t=0时将带电粒子从紧临B板处无初速释放,粒子到达A板时动量的大小;
,在t=0时将带电粒子从紧临B板处无初速释放,粒子到达A板时动量的大小;
(3)A板电势变化频率多大时,在 到
到 时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板.
时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板.
如图所示,真空中水平放置的两个相同极板Y和Y'长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出. 
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
如图计算机键盘上的每一个按键下面都有一个电容传感器。电容的计算公式是 ,其中常量ε=9。0×10-12Fm-1,S表示两金属片的正对面积,d表示两金属片间的距离。当某一键被按下时,d发生改变,引起电容器的电容发生改变,从而给电子线路发出相应的信号。已知两金属片的正对面积为50mm2,键未被按下时,两金属片间的距离为0。60mm。只要电容变化达0.25pF,电子线路就能发出相应的信号。那么为使按键得到反应,至少需要按下多大距离?
,其中常量ε=9。0×10-12Fm-1,S表示两金属片的正对面积,d表示两金属片间的距离。当某一键被按下时,d发生改变,引起电容器的电容发生改变,从而给电子线路发出相应的信号。已知两金属片的正对面积为50mm2,键未被按下时,两金属片间的距离为0。60mm。只要电容变化达0.25pF,电子线路就能发出相应的信号。那么为使按键得到反应,至少需要按下多大距离?
如图所示, 是匀强电场中的三点,并构成一等边三角形,每边长为
是匀强电场中的三点,并构成一等边三角形,每边长为 ,将一带电量
,将一带电量 的电荷从a点移到b点,电场力做功
的电荷从a点移到b点,电场力做功 ;若将同一点电荷从a点移到c点,电场力做功W2=6×10-6J,试求匀强电场的电场强度E。
;若将同一点电荷从a点移到c点,电场力做功W2=6×10-6J,试求匀强电场的电场强度E。