潮汐能是一种有待开发新能源，利用涨、落潮位差，可以把潮汐势能转化为动能再通过水轮机发电。如图所示为双向型潮汐电站示意图，在海湾建一拦水坝，使海湾与大海隔开构成水库, 在坝上安装水轮发电机组，利用潮汐造成的坝内、外水位差, 引导高水位的海水通过水轮发电机, 将机械能转变成电能。海水密度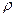
=1.0
103 kg/m2, g =10m/s2。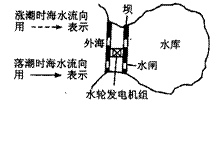
(1)试用图中规定的符号，画出涨潮和落潮时，海水双向流动的路径。
(2)已知某潮汐电站海湾水库面积约2.5106 m2, 假设电站的总能量转换效率为10% ，该电站的年发电总量1.0
107 kW·h ，电站发电功率为3.2103 kW。试推算出大坝两侧涨、落潮的平均潮差及日满负荷工作的时间。
A、B两船平行逆向贴近航行，当两船首尾对齐时，从每只船上各自以垂直航向向另一船投去质量为50 kg的物体.这时原来质量500 kg的A船停了下来，而质量为1 000 kg的B船仍沿原方向以8.5 m/s的速度航行，求两船原来的速度.
某一核反应的模型中质量为m0、速度为v0的粒子与一个质量为M、静止的原子核碰撞后合为一体，又迅速发生变化放出质量为m、速度为v的另一个粒子，此粒子的速度v与v0反方向.试问余下的反冲核的反冲速度为多大?
在太空中有一枚相对太空站以速度v0飞行的火箭，总质量为M，火箭突然向后喷出质量为m的气体：(1)若气体相对太空站的速度为u，则火箭的速度变为多少？(2)若气体相对火箭的速度为u，则火箭的速度变为多少？
气功碎石表演中，质量M="200" kg的石板压在演员身上，另一个演员举起质量m="5" kg的铁锤，使劲地向石板砸去的瞬间，石板被砸碎了，而演员安然无恙.试通过分析和必要的理论计算来说明其中的奥妙.
最初斜面和木箱均静止，后来木箱自光滑斜面滑下，如图16-10所示，木箱和斜面的质量分别为m="10" kg和M="50" kg，斜面长L="2" m,不计斜面与地面的摩擦，斜面倾角为30°.求木箱滑至斜面底部时斜面移动的距离.
图16-10