为了测量一个阻值较大的末知电阻,某同学使用了干电池(1.5V),毫安表(1mA),电阻箱(0~9999W),电键,导线等器材。该同学设计的实验电路如图甲所示,实验时,将电阻箱阻值置于最大,断开,闭合,减小电阻箱的阻值,使电流表的示数为I1=1.00mA,记录电流强度值;然后保持电阻箱阻值不变,断开,闭合,此时电流表示数为,记录电流强度值。由此可得被测电阻的阻值为W。
经分析,该同学认为上述方案中电源电动势的值可能与标称值不一致,因此会造成误差。为避免电源对实验结果的影响,又设计了如图乙所示的实验电路,实验过程如下:
断开,闭合,此时电流表指针处于某一位置,记录相应的电流值,其大小为I;断开,闭合,调节电阻箱的阻值,使电流表的示数为,记录此时电阻箱的阻值,其大小为。由此可测出= 。

在“验证机械能守恒定律”的实验中,所用电源的频率为50Hz,某同学选择了一条理想的纸带,用刻度尺测量时各计数点位置对应刻度尺上的读数如图所示,(图中O是打点计时器打的第一个点,A、B、C、D是间隔一段所取的点,图中单位为厘米),根据实验并结合纸带回答以下问题:
(1)现有器材是:电磁打点计时器;低压交流电源;纸带;带夹子的重物;刻度尺;天平;导线;铁架台。其中该实验不需要的器材是 __________;
(2)实验时,释放纸带与接通电源的合理顺序是______________________________;
(3)实验中,要从几条打上点的纸中挑选第一、二两点间的距离接近______mm并且点迹清晰的纸带进行测量。
(4)由纸带计算重锤下落的加速度为_________m/s2;(注:4、5、6三题保留两位小数)
(5)若重锤质量为m kg,则重锤从开始下落到B点时,减少的重力势能为_________;
(6)若重锤质量为m kg,则重锤从开始下落到B点时,重锤的动能为_____________。
(1)图中给出的是用螺旋测微器测量一金属薄板厚度时的示数,此读数应为mm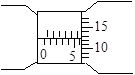
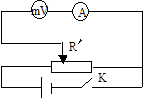
(2)实验室内有一电压表 ,量程为150mV 内阻约为150Ω 。现要将其改装成量程为10mA 的电流表。为此,实验室提供如下器材:干电池E(电动势为 1.5V ),滑线变阻器Rˊ,电流表
,量程为150mV 内阻约为150Ω 。现要将其改装成量程为10mA 的电流表。为此,实验室提供如下器材:干电池E(电动势为 1.5V ),滑线变阻器Rˊ,电流表 (有1.5mA , 15mA 与150mA 三个量程)及开关K。
(有1.5mA , 15mA 与150mA 三个量程)及开关K。
对电流表改装时必须知道电压表的内阻。可用图示的电路测量电压表 的内阻。在既不损坏仪器又能使精确度尽可能高的条件下,电路中的电流表
的内阻。在既不损坏仪器又能使精确度尽可能高的条件下,电路中的电流表 应选用的量程是。若合上K,调节滑线变阻器后测得电压表的读数为150mV,电流表
应选用的量程是。若合上K,调节滑线变阻器后测得电压表的读数为150mV,电流表 的读数为1.05mA,则电压表的内阻RmV为Ω。(取三位有效数字)
的读数为1.05mA,则电压表的内阻RmV为Ω。(取三位有效数字)
一弹簧振子悬挂在一列静止的火车上,振动的位移—时间图线如图所示。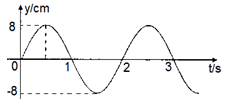
求:
(1)t=2s时,振子的振动方向;
(2)0~2s内,振子运动的路程;
(3)若火车水平匀速行驶,每节铁轨的长度为12m,则火车速度多大时,弹簧振子受迫振动的振幅最大?
在一根横绳上悬挂4个双线摆,其中A与B摆长相等,当使A自由摆动起来后,其它几个摆也随之摆动,周期分别设为TA、TB、TC、TD,则周期间的大小关系是,B、C、D中摆幅最大的是。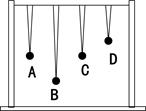
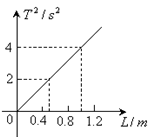
班级兴趣小组计划探究单摆周期与摆长的关系:
(1)已知摆球的直径为2cm,测得某次单摆竖直悬挂时,悬点对齐“0”刻度,下端刻度尺读数如图,则该单摆摆长为mm 。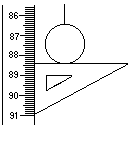
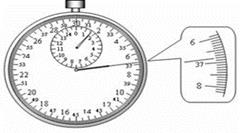
(2)在某次测量周期时,在停表上记录了摆动50次的时间如图,则摆动周期是s(保留三位有效数字)
(3)将记录数据描绘到T2—L图像上,该图像斜率的意义是,当地的重力加速度g = m/s2