(本小题共14分)
已知双曲线 的离心率为
的离心率为 ,右准线方程为
,右准线方程为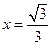
(Ⅰ)求双曲线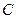 的方程;
的方程;
(Ⅱ)设直线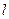 是圆
是圆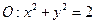 上动点
上动点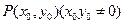 处的切线,
处的切线,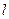 与双曲线
与双曲线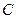 交于不同的两点
交于不同的两点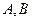 ,证明
,证明 的大小为定值.
的大小为定值.
(本小题满分14分)已知函数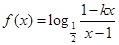 为奇函数.
为奇函数.
(1)求常数k的值;
(2)若 ,试比较
,试比较 与
与 的大小;
的大小;
(3)若函数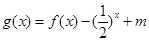 ,且
,且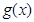 在区间
在区间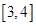 上没有零点,求实数m的取值范围.
上没有零点,求实数m的取值范围.
(本小题满分13分)已知二次函数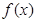 的最小值为1,且
的最小值为1,且 ,
,
(1)求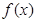 的解析式;
的解析式;
(2)若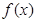 在区间
在区间 上不单调,求实数
上不单调,求实数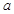 的取值范围;
的取值范围;
(3)在区间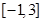 上,
上,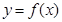 的图像恒在
的图像恒在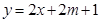 的图像上方,试确定实数
的图像上方,试确定实数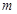 的取值范围.
的取值范围.
(本小题满分12分)某医药研究所研发了一种新药,如果成年人按规定的计量服用,据监测:服药后每毫升血液中的含药量 (微克)与时间
(微克)与时间 (时)之间近似满足如图所示的曲线。
(时)之间近似满足如图所示的曲线。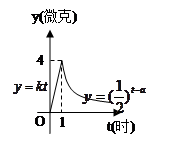
(1)写出服药后 与
与 之间的函数关系式
之间的函数关系式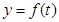 ;
;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效。试求服药一次治疗疾病的有效时间。
(本小题满分12分)若 ,求函数
,求函数 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)计算:
(1)
(2)