一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件个数,现观测得到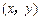 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).
(1)假定y与x之间有线性相关关系,求y对x的回归直线方程;
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒.(精确到1转/秒)
(本小题满分12分)在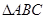 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知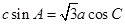 .
.
(Ⅰ)求C;
(Ⅱ)若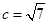 ,且
,且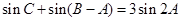 ,求
,求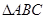 的面积.
的面积.
(满分12分)已知函数 的单调递减区间是(1,2),且满足
的单调递减区间是(1,2),且满足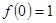 。
。
(1)求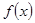 的解析式;
的解析式;
(2)对任意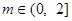 ,关于
,关于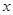 的不等式
的不等式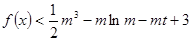 在
在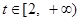 上有解,求实数
上有解,求实数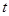 的取值范围。
的取值范围。
(满分12分)已知圆O: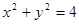 ,点P在直线
,点P在直线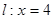 上的动点。
上的动点。
(1)若从P到圆O的切线长为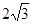 ,求P点的坐标以及两条切线所夹劣弧长;
,求P点的坐标以及两条切线所夹劣弧长;
(2)若点A(-2,0),B(2,0),直线PA,PB与圆O的另一个交点分别为M,N,求证:直线MN经过定点(1,0)。
(满分12分)定义在R上的奇函数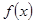 有最小正周期4,且
有最小正周期4,且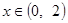 时,
时,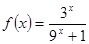 。
。
(1)求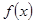 在
在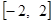 上的解析式;
上的解析式;
(2)判断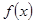 在(0,2)上的单调性,并给予证明;
在(0,2)上的单调性,并给予证明;
(3)当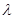 为何值时,关于方程
为何值时,关于方程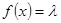 在
在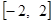 上有实数解?
上有实数解?
(满分12分) 是等差数列
是等差数列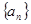 的前
的前 项和,
项和, ,
, 。
。
(1)求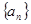 的通项公式;
的通项公式;
(2)设 (
(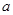 是实常数,且
是实常数,且 ),求
),求 的前
的前 项和
项和 。
。