设想宇航员完成了对火星表面的科学考察任务,乘坐返回舱返回围绕火星做圆周运动的轨道舱,如图所示.为了安全,返回舱与轨道舱对接时,必须具有相同的速度.求该宇航员乘坐的返回舱至少需要获得多少能量,才能返回轨道舱?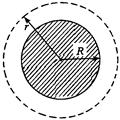
已知:返回过程中需克服火星引力做功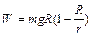 ,返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r;不计火星表面大气对返回舱的阻力和火星自转的影响.
,返回舱与人的总质量为m,火星表面重力加速度为g,火星半径为R,轨道舱到火星中心的距离为r;不计火星表面大气对返回舱的阻力和火星自转的影响.
如图在直角坐标XOY的第一象限内有竖直向下的匀强电场E=0.5V/m,垂直纸面向里的边界与X轴平行的匀强磁场B=0.4T,一开口向上光滑绝缘圆筒内有一内径略小的带正电小球m=1kg,q=+10C,圆筒的长度与匀强磁场的宽度相等,由O点开始,圆筒向右以v0=5m/s匀速直线运动,经过一段时间,圆筒运动到P点(P在磁场上边界)时小球恰好滑出筒口并且有了与X轴正向夹角θ=600斜向上的速度,之后小球在电场中运动,重力加速度取10m/s2求:小球再次回到与P点等高时的坐标值?
空间某区域有相互平行的匀强电场和匀强磁场,已知电场强度E,方向竖直向下,磁场在图中未画出,现由上向下观察一带电的单摆沿顺时针做匀速圆周运动,并且在t时间内运行了n周,已知小球的质量为m,摆线长为L,重力加速度为g,试求:
(1)小球带何种电荷,电量是多少?
(2)磁感应强度B的大小和方向?
(3)若突然撤去匀强磁场,小球将做什么运动?绳中的张力是多大?
水平光滑轴上用长L的轻绳静止悬挂一小球,t=0时刻,对小球施加一瞬时水平向右的冲量I1。当t=3T时,再次给小球施加一与I1同方向的瞬时冲量I2,小球才恰好能到达最高点。已知小球始终在圆周上运动,求(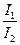 )的最大值?
)的最大值?
如图所示, 半径为r,质量不计的圆盘盘面与地面相垂直, 圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点的正下方离O点r/2处固定一个质量也为m的小球B. 放开盘让其自由转动, 问 :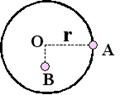
A球转到最低点时的线速度是多少?
在转动过程中半径OA向左偏离竖直方向的最大角度是多少?
如图5-3-8所示,光滑坡道顶端距水平面高度为h,质量为m的小物块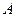 从坡道顶端由静止滑下,进入水平面上的滑道时无机械能损失,为使
从坡道顶端由静止滑下,进入水平面上的滑道时无机械能损失,为使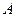 制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端恰位于滑道的末端O点。已知在OM段,物块A与水平面间的动摩擦因数均为
制动,将轻弹簧的一端固定在水平滑道延长线M处的墙上,另一端恰位于滑道的末端O点。已知在OM段,物块A与水平面间的动摩擦因数均为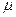 ,其余各处的摩擦不计,重力加速度为g,求:
,其余各处的摩擦不计,重力加速度为g,求:物块速度滑到O点时的速度大小;
弹簧为最大压缩量d时的弹性势能(设弹簧处于原长时弹性势能为零)
若物块
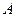 能够被弹回到坡道上,则它能够上升的最大高度是多少?
能够被弹回到坡道上,则它能够上升的最大高度是多少?