已知函数 ,若存在
,若存在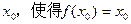 ,则
,则
称是函数 的一个不动点,设
的一个不动点,设
(Ⅰ)求函数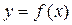 的不动点;
的不动点;
(Ⅱ)对(Ⅰ)中的二个不动点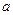 、
、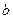 (假设
(假设 ),求使
),求使
恒成立的常数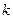 的值;
的值;
已知向量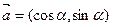 ,
, .
.
(1)若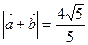 ,求
,求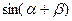 的值;
的值;
(2)若 且
且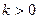 ,求
,求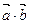 的最小值及此时向量
的最小值及此时向量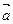 与
与 所成角的大小.
所成角的大小.
某单位建造一间背面靠墙的小房,地面面积为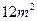 ,房屋正面每平方米的造价为
,房屋正面每平方米的造价为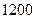 元,房屋侧面每平方米的造价为
元,房屋侧面每平方米的造价为 元,屋顶的造价为
元,屋顶的造价为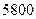 元.如果墙高为
元.如果墙高为 ,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低造价是多少?
,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低造价是多少?
已知向量 满足
满足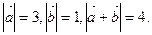
求(1)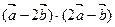 ;
;
(2)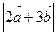 .
.
已知数列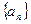 是一个等差数列,且
是一个等差数列,且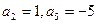 .
.
(1)求数列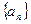 的通项
的通项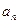 ;
;
(2)求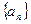 的前
的前 项和
项和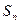 .
.
(本小题满分12分)已知函数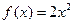 ,
,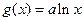
 ,点
,点 是函数
是函数 图象上任意一点,直线
图象上任意一点,直线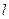 为函数
为函数 的图象在点
的图象在点 处的切线.
处的切线.
(Ⅰ)求直线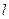 的方程;
的方程;
(Ⅱ)若存在点 ,使得直线
,使得直线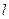 与函数
与函数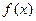 的图象相切,求
的图象相切,求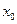 和
和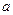 的取值范围;
的取值范围;
(Ⅲ)若对于任意直线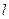 都不能与函数
都不能与函数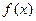 的图象相切,
的图象相切,
求证: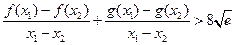 (其中
(其中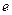 为自然对数的底数).
为自然对数的底数).