提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆 /千米)的函数,当桥上的车流密度达到200辆 /千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆 /千米时,车流速度为60千米/小时,研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当 时,求函数的表达式;
时,求函数的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最大值. (精确到1辆/小时).
可以达到最大,并求出最大值. (精确到1辆/小时).
已知等差数列{a n}的首项a 1=1,公差d>0,且其第二项、第五项、第十四项分别是等比数列{b n}的第二、三、四项.
(1)求数列{a n}与{b n}的通项公式;
(2)令数列{c n}满足:c n= 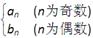 ,求数列{c n}的前101项之和T 101;
,求数列{c n}的前101项之和T 101;
(3)设数列{c n}对任意n∈N*,均有 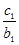 +
+ 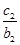 +…+
+…+ 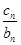 =a n +1成立,求c 1+c 2+…+c 2012的值.
=a n +1成立,求c 1+c 2+…+c 2012的值.
已知A(0,3)、B(-1,0)、C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
在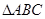 中,
中,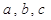 分别是角
分别是角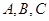 的对边长.已知a=2,
的对边长.已知a=2,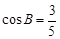 .
.
(1)若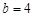 ,求
,求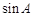 的值; (2)若
的值; (2)若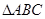 的面积
的面积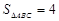 ,求
,求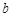 ,
,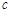 的值.
的值.
(1)解不等式: 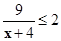 (见课本71页)
(见课本71页)
(2)已知不等式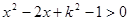 对一切实数
对一切实数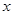 恒成立,求实数
恒成立,求实数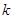 的取值范围.
的取值范围.