定义在R上的奇函数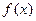 有最小正周期4,且
有最小正周期4,且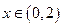 时,
时,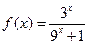 。求
。求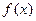 在
在 上的解析式
上的解析式
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.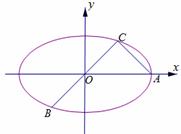
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: 为定值.
为定值.
如图所示的多面体中, 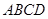 是菱形,
是菱形,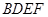 是矩形,
是矩形,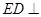 平面
平面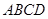 ,
,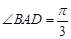 ,
,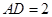 .
.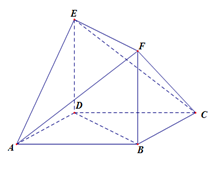
(1)求证:平面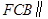 平面
平面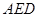 ;
;
(2)若二面角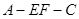 为直二面角,求直线
为直二面角,求直线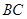 与平面
与平面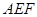 所成的角
所成的角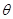 的正弦值.
的正弦值.
某校高一年级60名学生参加数学竞赛,成绩全部在40分至100分之间,现将成绩分成以下6段: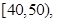
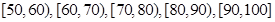 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 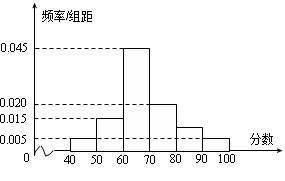
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于80分的学生中随机选3名学生,其中成绩在[90,100]内的学生人数为ξ,求ξ的分布列与均值.
已知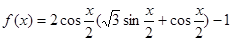 ,
,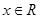 .
.
⑴ 求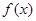 的最小正周期;
的最小正周期;
⑵设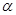 、
、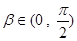 ,
,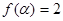 ,
,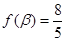 ,求
,求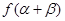 的值.
的值.
从数列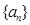 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列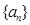 的一个子列.
的一个子列.
(1)写出数列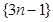 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设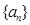 是无穷等比数列,首项
是无穷等比数列,首项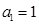 ,公比为
,公比为 .求证:当
.求证:当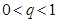 时,数列
时,数列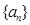 不存在
不存在
是无穷等差数列的子列.