如图所示,恒定的拉力大小F=8N,方向与水平线夹θ=60°角,拉着绳头使物体沿水平面移动 =2m的过程中,拉力做了多少功?
=2m的过程中,拉力做了多少功?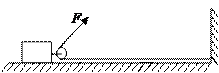
如图所示,用细绳AO、BO、CO悬挂一重物,AO、BO、CO所能承受的最大拉力均为100N,已知BO处于水平,∠AOB =150°,为了保证悬绳都不断,所挂重物最多不能超过多少?
质量为1.5t的汽车在前进中受到的阻力是车重的0.05倍,汽车在水平地面上做匀加速直线运动时,5s内速度由36km/h增加到54km/h。求汽车发动机的牵引力的大小(g取10m/s2)
月球中心到地球中心的距离大约是地球半径的60倍,如果地球表面的重力加速度为 试求:
试求:
(1)地球的引力使月球具有的加速度;
(2)月球绕地球做匀速圆周运动的线速度。
静电场与引力场有着非常相似的性质,力的形式都遵从平方反比定律,解答下列问题:
(1)写出万有引力定律和库仑定律中的常数G与K的单位。
(2)某星球的质量为M,在该星球表面某一倾角为θ的山坡上以初速度v0平抛一个物体,经 时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?
时间该物体落到山坡上。欲使该物体不再落回该星球的表面,至少应以多大的速度抛出物体(不计一切阻力,万有引力常量为G)?
(3)如图所示,质量为m的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为q,在杆上B点处固定一个电量为Q的正电荷。将A由距B竖直高度为H处无初速释放,小球A下滑过程中电量不变。不计A与细杆间的摩擦,整个装置处在真空中。已知静电力恒量k和重力加速度g,求:A球刚释放时的加速度以及当A球的动能最大时,A球与B点的距离。
)如图所示,一个内外半径均可看作R= 、光滑绝缘且竖直放置的细圆管,处于水平方向的匀强电场和匀强磁场内,电场与管道平面平行向左,磁场垂直管道平面向里。一个带正电的小球置于细圆管内,其所受电场力是重力的
、光滑绝缘且竖直放置的细圆管,处于水平方向的匀强电场和匀强磁场内,电场与管道平面平行向左,磁场垂直管道平面向里。一个带正电的小球置于细圆管内,其所受电场力是重力的 倍,现在最高点P给该小球一水平向左的初速
倍,现在最高点P给该小球一水平向左的初速 ,恰好使小球在细圆管内做完整的圆周运动。
,恰好使小球在细圆管内做完整的圆周运动。
(1)求初速度 ;
;
(2)在整个运动过程中,小球的最大速度多大?
(3)如果在最高点P时,小球对轨道的压力是重力的0.6倍,则小球运动到最低点时,它对轨道的压力是其重力的多少倍?