小敏探究了串联电路和并联电路的电压关系和电流关系后,对如图13-19甲所示既有并联又有串联的电路的电流关系提出了猜想:总电流等于各支路电流之和.
为验证猜想,小敏设计如图3-19甲所示的电路,用图乙所示器材做了三次实验,记录数据如表所示.
| 电表 次数 |
A1(A) |
A2(A) |
A3(A) |
V1(V) |
V2(V) |
V3(V) |
| 1 |
1.2 |
0.8 |
2.0 |
12.0 |
6.0 |
18.0 |
| 2 |
0.9 |
0.6 |
1.5 |
9.0 |
9.0 |
18.0 |
| 3 |
0.6 |
0.4 |
1.0 |
6.0 |
12.0 |
18.0 |
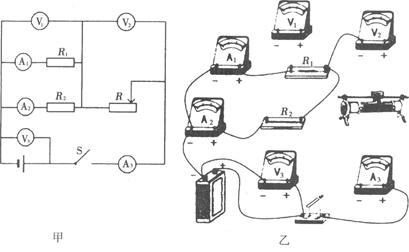
图3-19
请完成:(1)用笔画线代替导线,按图3-19甲的电路将图3-19乙的实物连线补充完整;
(2)为验证猜想,应选用电表 的示数进行比较;
(3)比较表中三个电压表的示数,可得到的结论是 ;
(4)认真分析小敏的实验数据,还可以得到很多规律,请你写出其中的一个(不能与猜想和(3)结论重复).
规律: 。
如图所示,质量为M=0.5kg的框架B放在水平地面上。劲度系数为k=100N/m的轻弹簧竖直放在框架B中,轻弹簧的上端和质量为m=0.2kg的物体C连在一起。轻弹簧的下端连在框架B的底部。物体C在轻弹簧的上方静止不动。现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就在框架B中上下做简谐运动。在运动过程中,框架B始终不离开地面,物体C始终不碰撞框架B的顶部。已知重力加速度大小为g=10m/s2。试求:当物体C运动到最低点时,物体C的加速度大小和此时物体B对地面的压力大小。
如图所示,长为31cm、内径均匀的细玻璃管开口向上竖直放置,管内水银柱的上端正好与管口齐平,封闭气体的长为10cm,,外界大气压强不变.若把玻璃管在竖直平面内缓慢转至开口竖直向下,这时留在管内的水银柱长为15cm,然后再缓慢转回到开口竖直向上,求:
(1)大气压强p0的值;
(2)玻璃管重新回到开口竖直向上时空气柱的长度;
如图所示,s为一电子发射枪,可以连续发射电子束,发射出来的电子初速度可视为0,电子经过平行板A、B之间的加速电场加速后,从O点沿x轴正方向进入xoy平面内,在第一象限内沿x、y轴各放一块平面荧光屏,两屏的交点为O,已知在y>0、0<x<a的范围内有垂直纸面向外的匀强磁场,在y>0、x>a的区域有垂直纸面向里的匀强磁场,大小均为B。已知给平行板AB提供直流电压的电源E可以给平行板AB提供0~U之间的各类数值的电压,现调节电源E的输出电压,从0调到最大值的过程中发现当AB间的电压为 时,x轴上开始出现荧光。(不计电子的重力)试求:
时,x轴上开始出现荧光。(不计电子的重力)试求:
(1)当电源输出电压调至 和U时,进入磁场的电子运动半径之比r1:r2
和U时,进入磁场的电子运动半径之比r1:r2
(2)两荧光屏上的发光亮线的范围。
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为30º足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图为通过计算机绘制出的滑块上滑过程中的v-t图。最大静摩擦力可视为等于滑动摩擦力,g取10m/s2,求:
(1)滑块冲上斜面过程中的加速度大小;
(2)滑块与斜面间的动摩擦因数;
(3)判断滑块最后能否返回斜面底端?若能返回,求出返回斜面底端时的动能;若不能返回,求出滑块停在什么位置。
如图所示,在直角坐标系xoy平面的第Ⅱ象限内有半径为r的圆o1分别与x轴、y轴相切于C(-r,0)、D(0,r) 两点,圆o1内存在垂直于xoy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于G点,一带正电的A粒子(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从C点射入磁场,经磁场偏转恰好从D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求: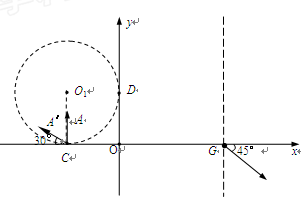
(1)A粒子在磁场区域的偏转半径及OG之间的距离;
(2)该匀强电场的电场强度E;
(3)若另有一个与A的质量和电荷量均相同、速率也相同的粒子A′,从C点沿与x轴负方向成30°角的方向射入磁场,则粒子A′再次回到x轴上某点时,该点的坐标值为多少?