为赢的2010年上海世博会的制高点,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值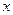 (单位:元,
(单位:元,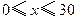 )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成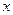 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
是否存在实数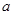 ,使得函数
,使得函数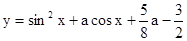 在闭区间
在闭区间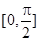 上的最大值是1?若存在,求对应的
上的最大值是1?若存在,求对应的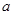 值?若不存在,试说明理由.
值?若不存在,试说明理由.
已知函数f(x)=sin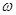 x(
x(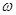 >0).
>0).
(1)若y=f(x)图象过点(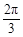 ,0),且在区间(0,
,0),且在区间(0,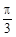 )上是增函数,求
)上是增函数,求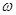 的值.
的值.
(2)先把(1)得到的函数y=f(x)图象上各点的纵坐标伸长为原来的2倍,(横坐标不变);再把所得的图象向右平移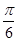 个单位长度,设得到的图象所对应的函数为
个单位长度,设得到的图象所对应的函数为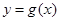 ,求当
,求当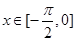 时,
时,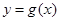 的最大和最小值。
的最大和最小值。
(1)设f(x)= (0<x<π),求函数f(x)的值域;
(0<x<π),求函数f(x)的值域;
(2)对任意的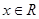 ,不等式
,不等式 恒成立,求
恒成立,求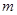 的取值范围
的取值范围
如图,A,B是海面上位于东西方向相距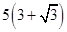 海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距
海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距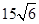 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?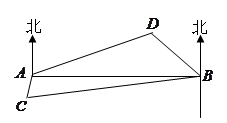
在△ABC中,已知
(1)求 的值;
的值;
(2)求角