已知n是正偶数,用数学归纳法证明时,若已假设n=k(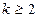 且为偶数)时命题为真,,则还需证明()
且为偶数)时命题为真,,则还需证明()
| A.n=k+1时命题成立 | B.n=k+2时命题成立 |
| C.n=2k+2时命题成立 | D.n=2(k+2)时命题成立 |
已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是()
A  B
B 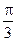 C
C 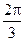 D
D 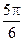
已知双曲线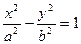 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
| A.( 1,2) | B.(1,2) | C.[2,+∞] | D.(2,+∞) |
已知P是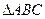 内一点,且满足
内一点,且满足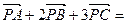 0,记
0,记
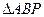 、
、 、
、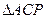 的面积依次为
的面积依次为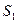 、
、 、
、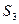 ,则
,则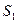 :
: :
: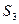 等于()
等于()
| A.1:2:3 | B.1:4:9 | C. : :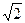 :1 :1 |
D.3:1:2 |
口袋里放有大小相同的2个红球和1个白球,有放回的每次模取一个球,定义数列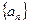 :
: .如果
.如果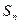 为数列
为数列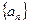 的前n项之和,那么
的前n项之和,那么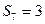 的概率为()
的概率为()
A.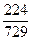 |
B.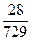 |
C. |
D.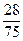 |
设定义域为 函数
函数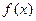 满足
满足 且当
且当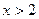 时,
时,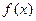 单调递增,如果
单调递增,如果 且
且 ,则
,则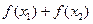 的值()
的值()
| A.恒小于0 | B.恒大于0 | C.可能为0 | D.可正可负 |