早在19世纪，匈牙利物理学家厄缶就明确指出：“沿水平地面向东运动的物体，其重量（即：列车的视重或列车对水平轨道的压力）一定要减轻。”后来，人们常把这类物理现象称为“厄缶效应”。如图1所示：我们设想，在地球赤道附近的地平线上，有一列质量是m的列车，正在以速率v，沿水平轨道匀速向东行驶。已知：（1）地球的半径R；（2）地球的自转周期T。今天我们象厄缶一样，如果仅考虑地球自转的影响（火车随地球做线速度为
R/T的圆周运动）时，火车对轨道的压力为N；在此基础上，又考虑到这列火车匀速相对地面又附加了一个线速度v做更快的圆周运动，并设此时火车对轨道的压力为N/，那么单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量（N－N/）为 （ ）
A． |
B． |
C． |
D． |
如图（a）所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图像如图（b）所示，若重力加速度g取10m/s2．根据图（b）中所提供的信息可以计算出（）
| A．物体的质量 |
| B．斜面的倾角 |
| C．加速度为6m/s2时物体的速度 |
| D．加速度由2m/s2增加到6m/s2 的过程中物体通过的位移 |
质量为2kg的物体静止在足够大的水平地面上，物体与地面间的动摩擦因数为0.2，最大静摩擦力与滑动摩擦力大小视为相等。从t＝0时刻开始，物体受到方向不变、大小呈周期性变化的水平拉力F作用，F随时间t的变化规律如图所示，重力加速度g取10m/s2，则物体在t＝0至t＝12s这段时间的位移大小为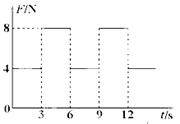
| A．18m | B．54m | C．72m | D．198m |
如图所示，一名消防队员在模拟演习训练中，沿着长为l2m的竖立在地面上的钢管往下滑。已知这名消防队员的质量为60kg，他从钢管顶端由静止开始先匀加速再匀减速下滑，滑到地面时速度恰好为零。如果他加速时的加速度大小是减速时的2倍，下滑的总时间为3s，g取10m/s2，那么该消防队员
| A．下滑过程中的最大速度为4 m/s |
| B．加速与减速过程的时间之比为1：2 |
| C．加速与减速过程中所受摩擦力大小之比为l：7 |
| D．加速与减速过程的位移之比为1：4 |
已知某一物体从楼顶自由落下,经过下面高为2.0m的窗户所用的时间为0.2s.（忽略空气的阻力）(取g=10m/s2)则物体从楼顶到窗台的距离为（）
| A． 4.05m | B．5m | C． 6.05m | D．6.5m |
如图所示，并排放在光滑水平面上的两物体的质量分别为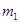
和
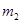，且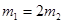
。在用水平推力F向右推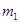时，两物体间的相互压力的大小为
，则
A． |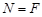
B． |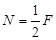
C． |
D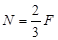． |