口袋里装有两个白球和两个黑球,这四个球除颜色外完全相同,四个人按顺序依次从中摸出一球,试求“第二个人摸到白球”的概率。
(本小题满分8分)
将圆心角为1200,面积为3 的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
设 ,函数
,函数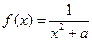 .
.
(Ⅰ)证明:存在唯一实数 ,使
,使 ;
;
(Ⅱ)定 义数列
义数列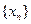 :
: ,
, ,
,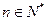 .
.
(i)求证:对任意正整数n都有 ;
;
(ii) 当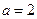 时,若
时,若 ,
,
证明:当k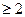 时,对任意
时,对任意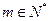 都有:
都有: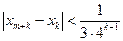
已知函数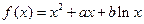 (
(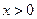 ,实数
,实数 ,
, 为常数).
为常数).
(Ⅰ)若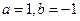 ,求函数
,求函数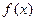 的极值;
的极值;
(Ⅱ)若 ,讨论函数
,讨论函数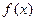 的单
的单 调性.
调性.
双曲线的中心为原点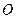 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为 ,经过右焦点
,经过右焦点
 垂直于
垂直于 的直线分别交
的直线分别交 于
于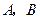 两点.已知
两点.已知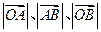 成等差数列,且
成等差数列,且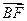 与
与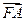 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ )设
)设 被双曲线所截
被双曲线所截 得的线段的长为4,求双曲线的方程.
得的线段的长为4,求双曲线的方程.
如图,在四棱锥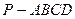 中,底面
中,底面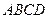 是矩形.
是矩形. 已知
已知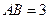
 .
.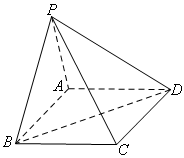
(Ⅰ)证明 平面
平面 ;
;
(Ⅱ)求异面直线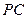 与
与 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角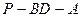
 的大小.
的大小.