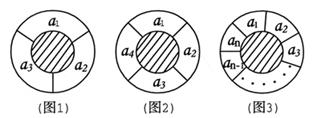
一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
(1)如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法? 

(2)如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
(本小题满分12分)
已知斜三棱柱ABC—A1B1C1的底面是正三角形,侧面ABB1A1是边长为2的菱形,且 ,M是AB的中点,
,M是AB的中点,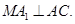
(1)求证: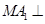 平面ABC;
平面ABC;
(2)求点M到平面AA1C1C的距离.
(本小题满分12分)
已知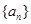 为等比数列,
为等比数列, 为等差数列
为等差数列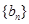 的前n项和,
的前n项和,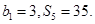
(1)求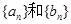 的通项公式;
的通项公式;
(2)设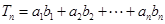 ,求
,求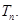
设函数 ,其中
,其中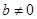 。
。
⑴当 时,判断函数
时,判断函数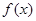 在定义域上的单调性;
在定义域上的单调性;
⑵求函数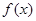 的极值点;
的极值点;
⑶证明对任意的正整数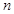 ,不等式
,不等式 成立。
成立。
如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
,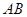 边所在直线的方程为
边所在直线的方程为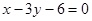 ,点
,点 在
在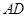 边所在直线上。
边所在直线上。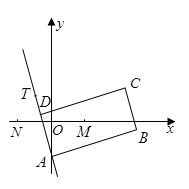
⑴求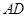 边所在直线的方程;
边所在直线的方程;
⑵求矩形 外接圆的方程;
外接圆的方程;
⑶若动圆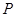 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆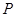 的圆心的轨迹方程。
的圆心的轨迹方程。
如图,甲船以每小时 海里的速度向正北方向航行,乙船按固定的方向匀速直线航行。当甲船位于
海里的速度向正北方向航行,乙船按固定的方向匀速直线航行。当甲船位于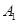 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西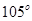 方向的
方向的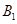 处,此时两船相距
处,此时两船相距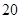 海里,当甲船航行
海里,当甲船航行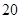 分钟到达
分钟到达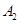 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西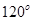 方向的
方向的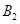 处,此时两船相距
处,此时两船相距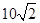 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?