如图所示,两根间距为L=1m的金属导轨MN和PQ,电阻不计,左端向上弯曲,其余水平,水平导轨左端有宽度为d=2m,方向竖直向上的匀强磁场i,右端有另一磁场ii,其宽度为d,但方向竖直向下,两者B均为1T,有两根质量均为m=1kg,电阻均为R=1Ω,的金属棒a与b与导轨垂直放置,b棒置于磁场ii中点C,D处,导轨除C,D外(对应距离极短)其余均为光滑,两处对棒可产生总的最大静摩擦力为自重的0.2倍,a棒从弯曲导轨某处由静止释放,当只有一根棒做切割磁感线运动时,它速度的减小量与它在磁场中通过的距离成正比,即Δv∝Δx
(1)若棒a从某一高度释放,则棒a进入磁场i时恰能使棒b运动,判断棒b运动方向并求出释放高度;
(2)若将棒a从高度为0.2m的某处释放结果棒a以1m/s的速度从磁场i中穿出求两棒即将相碰时棒b所受的摩擦力;
(3)若将棒a从高度1.8m某处释放经过一段时间后棒a从磁场i穿出的速度大小为4m/s,且已知棒a穿过磁场时间内两棒距离缩短2.4m,求棒a从磁场i穿出时棒b的速度大小及棒a穿过磁场i所需的时间(左为a,右为b)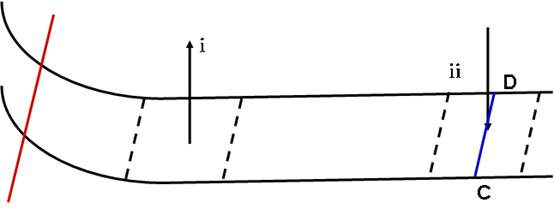
在如图所示电路中,已知R3=4 Ω,闭合开关,电流表读数为0.75 A,电压表读数为2 V,经过一段时间,一个电阻被烧坏(断路),使电流表读数变为0.8 A,电压表读数变为3.2 V,问: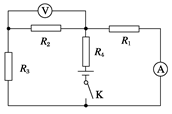
(1)哪个电阻发生断路故障?
(2)R1的阻值是多少?
(3)能否求出电源电动势E和内阻r?如果能,求出结果;如果不能,说明理由。
如图所示,在竖直向下的匀强电场中,一个质量为m带负电的小球从斜轨道上的A点由静止滑下,小球通过半径为R的圆轨道顶端的B点时恰好不落下来、已知轨道是光滑而又绝缘的,且小球的重力是它所受的电场力2倍,求: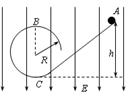
(1)A点在斜轨道上的高度h为多少?
(2)小球运动到最低点时对轨道的最小压力为多少?
一质量m=0.6kg的物体以v0=20m/s的初速度从倾角为30º的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=18J,机械能减少了ΔE=3J。不计空气阻力,重力加速度g=10m/s2,求:⑴物体向上运动时加速度的大小;⑵物体返回斜坡底端时的动能。
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=6.0×105 N/C,方向与x轴正方向相同,在O处放一个电荷量q=-5.0×10-8 C,质量m=1.0×10-2 kg的绝缘物块,物块与水平面间的动摩擦因数μ=0.20,沿x轴正方向给物块一个初速度v0=2.0 m/s,如图所示。(g取10 m/s2)试求:
(1)物块向右运动的最大距离;
(2)物块最终停止的位置。
跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距地面125 m时打开降落伞,开伞后运动员以大小为14.30 m/s2的加速度做匀减速运动,到达地面时的速度为5 m/s,求:
(1)运动员离开飞机瞬间距地面的高度;
(2)离开飞机后,经多长时间到达地面。(g取10m/s2)