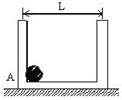
如图所示，水平面放一质量为0.5kg的长条形金属盒，盒宽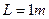
，它与水平面间的动摩擦因数是0.2，在盒的A端有一个与盒质量相等的小球。球与盒无摩擦，现在盒的A端迅速打击一下金属盒，给盒以
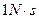的向右的冲量，设球与盒间的碰撞没有能量损失，且碰撞时间极短，求球与盒组成的系统从开始运动到完全停止所用时间。（
）
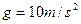如图10-1-21所示，线圈的面积是0.05 m2，共100匝，线圈电阻为r="1" Ω，外接电阻R="9" Ω，匀强磁场的磁感应强度
，当线圈以300 r/min的转速匀速旋转时，则：
图10-1-21
（1）若从线圈中性面开始计时，写出线圈中感应电动势瞬时值表达式.
（2）从中性面开始计时，线圈转过
时电动势瞬时值为多大？
（3）电路中电压表和电流表的示数各是多少？
（4）由图示位置转过60°角的过程产生的平均感应电动势为多少？
有一10匝正方形线框，边长为20 cm，线框总电阻为1 Ω，外接电阻R＝9 Ω，线框绕OO′轴以10π Rad/s的角速度匀速转动，如图10-1-13，垂直于线框平面向里的匀强磁场的磁感应强度为0.5 T.问：
图10-1-13
（1）该线框产生的交变电流电动势最大值是多少？
（2）线框从图示位置转过60°时，感应电动势的瞬时值是多大？
（3）写出感应电动势随时间变化的表达式.
（4）电路中电压表和电流表的示数各是多少？
如图10-1-12中的左右两个电路都是从左端输入信号，从右端输出信号.左图中输入的是高频、低频混合的交流信号，要求只输出低频信号；右图中输入的是直流和低频交流的混合信号，要求只输出低频交流信号.那么C1、C2中哪个该用大电容？哪个该用小电容？
图10-1-12
正弦交流电是由闭合线圈在匀强磁场中匀速转动产生的.线圈中感应电动势随时间变化的规律如图13-6所示，则此感应电动势的有效值为_________V，频率为_________Hz.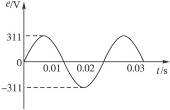
图13-6
如图13-1-4所示，矩形线框的匝数n=250匝，ab="12" cm,ad="10" cm，线框置于B=
T的匀强磁场中绕垂直于磁场的轴以120 r/min匀速转动，线框通过滑环与外电路相连，外电路接有R="12" Ω 的电阻及一只发光的电压为12 V的氖泡L，求：
图13-1-4
（1）当开关S接e时，A表的读数为多少？R的热功率为多大？10 min内外力对线框做功多少？
（2）当开关S接f时，氖泡的闪光频率为多大？通电10 min，氖泡发光的总时间为多少？（线框电阻不计）