先阅读理解下面的例题，再按要求解答：
例题：解一元二次不等式
.
解：∵
，
∴
.
由有理数的乘法法则“两数相乘，同号得正”，有
（1）
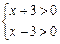（2）
解不等式组（1），得
，
解不等式组（2），得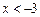
，
故的解集为或，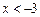
即一元二次不等式的解集为或.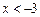
问题：求分式不等式
的解集.
一汽车厂生产
、
、
三类轿车，每类轿车均有舒适型和标准型两种型号,某月的产量如下表（单位：辆）
| 轿车 |
轿车 |
轿车 |
|
| 舒适型 |
 |
 |
 |
| 标准型 |
 |
 |
 |
按类型分层抽样的方法在这个月生产的轿车中抽取
辆，其中有类轿车
辆.
（1）求的值；
（2）用分层抽样的方法在类轿车中抽取一个容量为
的样本.将该样本看成一个总体，从中任取
辆，求至少有
辆舒适型轿车的概率；
（3）用随机抽样的方法从类舒适型轿车中抽取
辆，经检测它们的得分如下：
、
、
、
、
、
、
、
.把这辆轿车的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值
不超过
的概率.
如图，在三棱锥
中，
是等边三角形，
.
（1）证明:：
；
（2）证明：
；
（3）若
，且平面
平面
，求三棱锥体积.
在
中，内角
、
、
的对边分别为
、
、
，且
.
（1）求角的大小；
（2）若
，
，求的面积.
正四面体ABCD的体积为V，P是正四面体ABCD的内部的一个点．
(1)设“VPABC≥
V”的事件为X，求概率P(X)；
(2)设“VPABC≥V”且“VPBCD≥V”的事件为Y，求概率P(Y)．
“抛阶砖”是国外游乐场的典型游戏之一．参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上，抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠)，便可获大奖.不少人被高额奖金所吸引，纷纷参与此游戏但很少有人得到奖品，请用所学的概率知识解释这是为什么．