如图,在正方体 中,已知
中,已知 是棱
是棱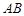 的中点.
的中点.
求证:(1)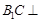 平面
平面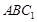 ,
,
(2)直线 ∥平面
∥平面 ;
;
一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.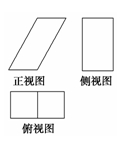
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
如图,在直三棱柱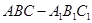 中,
中, ,
, 是棱
是棱 上的一点,
上的一点, 是
是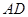 的延长线与
的延长线与 的延长线的交点,且
的延长线的交点,且 ∥平面
∥平面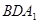 。
。
(1)求证: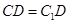 ;
;
(2)求二面角 的平面角的余弦值;
的平面角的余弦值;
(3)求点 到平面
到平面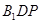 的距离.
的距离.
如图①,△BCD内接于直角梯形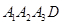 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.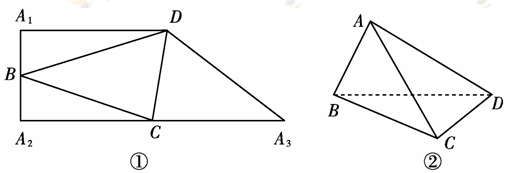
(1)求证:AB⊥CD;
(2)求直线BD和平面ACD所成的角的正切值;
(3)求四面体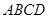 的体积。
的体积。
如图,在四棱锥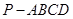 中,
中,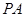 ⊥面
⊥面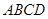 ,
,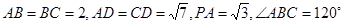
 为线段
为线段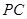 上的点.
上的点.
(Ⅰ)证明: ⊥面
⊥面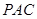 ;
;
(Ⅱ)若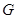 是
是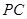 的中点,求
的中点,求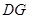 与
与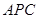 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若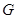 满足
满足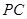 ⊥面
⊥面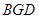 ,求
,求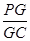 的值.
的值.