某发电站的输出功率为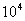 kW,输出电压为4kV,通过理想变压器升压后向80km远处供电。已知输电导线的电阻率为
kW,输出电压为4kV,通过理想变压器升压后向80km远处供电。已知输电导线的电阻率为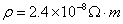 ,导线横截面积为
,导线横截面积为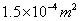 ,输电线路损失的功率为输出功率的4%,求:
,输电线路损失的功率为输出功率的4%,求:
(1)升压变压器的输出电压;
(2)输电线路上的电压损失。
一质点沿直线ox方向作加速运动,它离开o点的距离x随时间变化的关系为x=5+2t3(m),它的速度随时间变化的关系为v=6t2(m/s),求该质点在t=0到t=2s间的平均速度大小和t=2s到t=3s间的平均速度的大小。
如图所示为一物体沿直线运动x-t图象,根据图象求: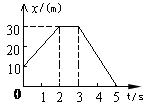
(1)第2s内的位移,第4秒内的位移,前5秒的总路程和位移
(2)各段的速度
(3)画出对应的v-t图象
汽车以36km/h的速度行驶,要求在紧急刹车时能在2s内停下来,则刹车时
的加速度大小至少是多少?
一竖直放置的水管,距地面高h=l.8m,管内横截面积S=2.0cm2。有水从管口处以不变的速度v=2.0m/s源源不断地流出,设出口处横截面上各处水的速度都相同,并假设水流在空中不散开,不计空气阻力。取重力加速度g=10m/s2。求水流稳定后在空中有多少立方米的水。
一宇宙空间探测器从某一星球的表面升空,假设探测器的质量恒为1500kg,发动机推力为恒力,探测器升空到某一高度时,发动机突然关闭,如图是表示其速度随时间变化规律:
(1)升空后,9s.25s.45s时探测器的运动情况(指此时的速度)如何?
(2)求宇宙探测器在该行星表面所能到达的最大高度?
(3)计算该行星表面的重力加速度?