如图甲所示,在两平行金属板的中线OO′某处放置一个粒子源,粒子源沿OO′方向连续不断地放出速度v0=1.0×105m/s的带正电的粒子。在直线MN的右侧分布范围足够大的匀强磁场,磁感应强度B=0.01πT,方向垂直纸面向里,MN与中线OO′垂直。两平行金属板的电压U随时间变化的U-t图线如图乙所示。已知带电粒子的荷质比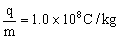 ,粒子的重力和粒子之间的作用力均可忽略不计,若t=0.1s时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
,粒子的重力和粒子之间的作用力均可忽略不计,若t=0.1s时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的)。求:
(1)在t=0.1s时刻粒子源放出的粒子离开电场时的速度大小和方向。
(2)从粒子源放出的粒子在磁场中运动的最短时间和最长时间。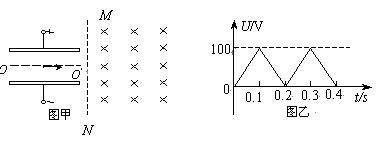
对于一定质量的理想气体,以p、V、T三个状态参量中的两个为坐标轴建立直角坐标系,在坐标系上描点能直观地表示这两个参量的数值.你能根据坐标系中不同点的位置来比较第三个参量的大小吗?图8-3-8三个坐标系中,两个点都表示相同质量某种理想气体的两个状态.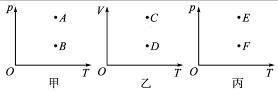
图8-3-8
(1)p-T图象中(图甲)A、B两个状态,哪个体积大?
(2)V-T图象中(图乙)C、D两个状态,哪个压强大?
(3)p-V图象中(图丙)E、F两个状态,哪个温度高?
请说出判断的根据.
钢筒内装有3 kg气体,当温度为-23 ℃时,压强为4 atm,如果用掉1 kg气体后温度升高到27 ℃,求筒内气体压强.
一活塞将一定质量的理想气体封闭在水平固定放置的气缸内,开始时气体体积为V0,温度为27℃.在活塞上施加压力,将气体体积压缩到2V0/3,温度升高到57℃.设大气压强P0=1.0×105 Pa,活塞与气缸壁摩擦不计.
(1)求此时气体的压强;
(2)保持温度不变,缓慢减小施加在活塞上的压力使气体体积恢复到V0,求此时气体的压强.
如图8-3-9所示,粗细均匀,两端开口的U形管竖直放置,管的内径很小,水平部分BC长14 cm.一空气柱将管内水银分离成左右两段.大气压强相当于高为76 cmHg的压强.
图8-3-9
(1)当空气柱温度为T0="273" K,长为l0="8" cm时,BC管内左边水银柱长2 cm,AB的管内水银柱长是2 cm,则右边水银柱总长是多少?
(2)当空气柱温度升高到多少时,左边的水银恰好全部进入竖直管AB内?
(3)当空气柱温度为490 K时,两竖直管内水银柱上表面高度各为多少?
如图8-3-12所示,一个密闭的气缸,被活塞分成体积相等的左、右两室,气缸壁与活塞是不导热的;它们之间没有摩擦,两室中气体的温度相等,现利用右室中的电热丝对右室加热一段时间,达到平衡后,左室的体积变为原来的 ,气体的温度T1="300" K,求右室气体的温度.
,气体的温度T1="300" K,求右室气体的温度.
图8-3-12