我们知道,验电器无法定量测定物体的带电量。学校实验室也没有其他定量测定电量的仪器。某研究性学习小组设计了一定量测定质量较小的小球带电量的方案如下:取两个完全相同的小球,用天平测出小球的质量m,然后让小球带上相同的电量Q,并将两个带电小球用相同的绝缘轻质细线如图所示悬挂(悬线长度远大于小球半径),测出稳定后悬线偏离竖直方向的夹角θ等物理量,从而算出小球的电量Q。你认为该设计方案是否可行,若可行,则还需测量哪些物理量才能求出小球所带的电量,用字母表示该物理量,并写出小球所带电量的表达式及其推导的过程。若不可行,请写出你的实验方案和相应的计算表达式及其推导过程。(已知静电力常量为K,当地重力加速度为g)
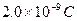
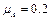
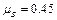
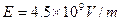
(1)A与B第一次碰前的瞬时A、B的速度分别是多大?
(2)从A开始运动到两物体第二次相碰经历多长时间?
(3)从开始撤去固定两物体的外力至第n次碰撞时A物体克服摩擦阻力做的功及电场力对B物体做的功?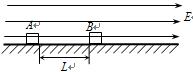
(1)子弹穿出木块时,木块获得的水平初速度V;
(2)木块落地点离桌面边缘的水平距离X;
(3)子弹打穿木块的过程,系统损失的机械能。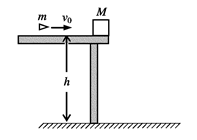

(1)甲球振动的振幅为多少?

(2)在甲球振动的过程中,弹簧最大的弹性势能为多少?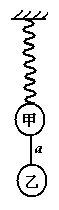
μ=0.4,且木块与桌面间的最大静摩擦力等于滑动摩擦力。
(1)要使木块由静止开始运动,至少要用多大水平拉力。
(2)用F1=6N的水平力拉木块,求木块受摩擦力的大小。
(3)木块在桌面滑动后,使水平拉力变为10N,木块受到的摩擦力是多大?